prawdopodobieństwo krokodyl: Pięćdziesięciu polityków zasiada do obrad przy okrągłym stole. Zakładamy ze uczestnicy negocjacji losują numerowane krzesła. Jakie jest prawdopodobienstwo tego ze prezes i dwóch wiceprezesów jednego z ugrupowań politycznych usiądą obok siebie ? może ktoś rozrysować tą sytuację?

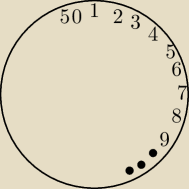
wredulus_pospolitus: Zakładam, że stół ma 50 miejsc. mają zasiąść obok siebie (nie jest podane w jakiej kolejności). Więc: prezes wybiera numer 50 możliwości wice nr 1 wybiera jeden z dwóch numerów obok prezesa − 2 możliwości wice nr 2 wybiera jeden z dwóch numerów obok kolegów − 2 możliwości + prezes wybiera numer 50 możliwości wice nr 1 wybiera jeden z dwóch numerów 'o jeden dalej' od prezesa − 2 możliwości wice nr 2 wybiera miejsce pomiędzy nimi − 1 możliwość

	50*2*2 + 50*2*1
P(A) =
	50*49*48

kerajs: Prezes wykorzystał swoje układy i wraz z wiceprezesami losują miejsca jako pierwsi. Prezes losuje i siada na wylosowanym miejscu. Lepszy wice losuje jako drugi i: a) na miejsce obok prezesa ma szanse 2/49, a wtedy gorszy wice na odpowiednie miejsce ma 2/48 szansy b) na miejsce odległe o dwa od prezesa ma szanse 2/49, a wtedy gorszy wice na odpowiednie miejsce ma 1/48 szansy

	2	2		2	1		6
P=			+			=
	49	48		49	48		48*49

krokodyl:

	3!*47!*50
w odpowiedziach mam
	50!

a w drugim zadaniu sześcioosobowa grupa dzieci o wyrównanych umiejętnościach pływackich bierze udział w wyścigu na 50m Można założyć że kolejność na mecie jest zupełnie przypadkowa zależna od chwilowej dyspozycji uczestników Jakie jest prawdopodobieństwo że Jaś i Małgosia ukończą wyścig zajmując dwie kolejne lokaty(nie zostaną przez nikogo przedzieleni)

	2!*4!*5
odp		i mam pytanie skoro to są analogiczne zadania to dlaczego w pierwszym jest
	6!

razy 50 w liczniku i 50! w mianowniku a nie *49

wredulus_pospolitus: Krokodyl −−− te trzy wyniki są sobie równe

krokodyl: wiem ale najłatwiej mi tym sposobem z książki bo to drugie zadanie zrobiłam tylko prościej było to rozrysować a tutaj w pierwszym mam problem i nie rozumiem tej części z 12:47

wredulus_pospolitus: różnica jest taka pomiędzy tymi zadaniami ... że w pierwszym mamy okrągły stół. I 3 miejsca zajmowane przez jednopartyjnych możemy rozważać w ten sposób (i tak zrobił autor zadania). Losujemy miejsce i dwa na prawo od niego −−− te trzy miejsca będą zajmowane przez nich na 3! sposobów (permutacja 3 osób). Jako, że stół jest okrągły to ów 3 miejsca można wybrać na 50 sposobów (bo od {1,2,3} do {50,1,2}) W drugim zadaniu masz 'początek' (pierwszy) i 'koniec' (ostatni) w wyścigu. związku z tym nie ma możliwości aby zajęcie 6 i 1 miejsca było takim, że Jaś i Małgosia zajęli dwie kolejne lokaty. Takich układów mamy 5 ({1,2} , {2,3} ,...,{5,6}) stąd '5' w liczniku.

krokodyl: dzięki już rozumiem a mam jeszcze jedno zadanie Obliczyć prawdopodobieństwo tego że trzy losowo wybrane wierzchołki sześcianu tworzą trójkąt równoboczny odp |A|=8 omega=(8) (3)

wredulus_pospolitus: ogólnie wzór można zapisać:

	n*(n−k)!*k!		n
P(A) =		=		przy okrągłym stole
	n!		n k

	(n−k+1)*(n−k)!*k!		n−k+1
P(B) =		=		przy ławce, kolejce, jakiejkolwiek
	n!		n k

linii/sznurku rzeczy/ludzi gdzie: n −−− ogólna liczba rzeczy i miejsc k −−− liczba rzeczy lub ludzi, które mają być 'obok siebie'

wredulus_pospolitus:

	8 3
rozumiem, że |Ω| =		tak Jeżeli tak, to tak

krokodyl: Ale dlaczego |A|=8 jak wybieramy trzy wierzchołki a nie osiem?

wredulus_pospolitus: bo tylko 8 trójkątów równobocznych można utworzyć

krokodyl: już rozumiem dzięki