Równania boków trójkąta Michal : Dane są dwa wierzchołki trójkąta A = (1, 3), B = (−1, 5) oraz punkt D = (2, 3), będący punktem przecięcia wysokości trójkąta. Równania boków tego trójkąta wynoszą

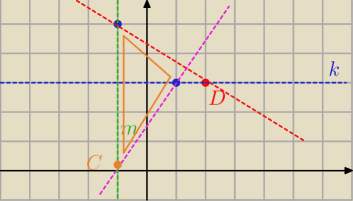
wredulus_pospolitus: 1. prowadzimy prostą k przechodzącą przez A i D 2. wyznaczamy prostą m, prostopadłą do k i przechodzącą przez B 3 i 4. analogicznie prostą przechodzącą przez B i D, a następnie do niej prostopadłą przechodzącą przez A 5. punkty (2) i (4) dają Ci dwa równania prostych zawierających boku (jeżeli masz wyznaczyć współrzedne punktu C, to przecięcie tych prostych da Ci wynik), ostatnia prosta −−− przechodzi przez A i B koooniec

Michal: Oo dzięki a mógłbyś to narysować bo muszę przyznać że jestem trochę zielony z tej geometrii

wredulus_pospolitus:

Michal: Dziękuję bardzo

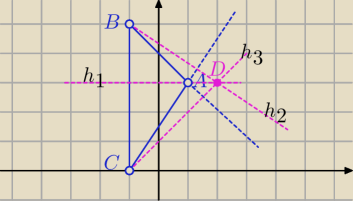
miś: wysokość h₁ zawiera się w prostej AD to h₁ ma równanie y=3 to prosta BC ⊥ h₁ to BC ma równanie BC: x= −1

	5−3		2		3
aBD=		= −		to aAC=		bo pr.BD⊥pr.AC
	−1−2		3		2

	3
więc prosta AC : y=		(x−1)+3 AC : y= 1,5x+1,5
	2

a_AB= −1 to pr. AB : y= −1(x−1)+ 3 AB : y= −x+4