Promień okręgu opisanego na pewnym trójkącie... Michał: Z 23 zadań, które zadała nam Pani nauczycielka jako przygotowanie do matury, nie byłem w stanie zrobić tego jednego. W internecie nie znalazłem tego zadania. Przyszło mi do głowy zaokrąglić sinus 0,4 i sinus 0,25 na wartość kąta w stopniach, ale wolałbym rozwiązać to zadanie bez zaokrąglania. Treść zadania Promień okręgu opisanego na pewnym trójkącie jest równy 10, a sinusy dwóch kątów tego trójkąta są równe 0,4 i 0,25. Oblicz pole tego trójkąta.

chichi: https://matematykaszkolna.pl/strona/549.html

Michał: Tak próbowałem już z tego wzoru. Obliczę a i obliczę b, ale nie jestem w stanie obliczyć trzeciego boku.

wredulus_pospolitus: znasz sinusy dwóch kątów ... możesz wyznaczyć sinus trzeciego kąta, korzystając z odpowiednich wzorów trygonometrycznych

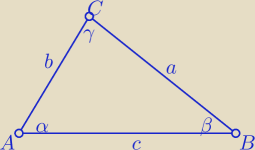
Eta: dł. boku c nie jest potrzebna do obliczenia pola tego trójkąta R= 10, sinα=0,4 sinβ= 0,25 sinγ= sin(α+β)= sinα*cosβ+cosα*sinβ cos²α=1− sin²α cos²β=1−sin²β cosα=.... cosβ=.... sinγ=.....

a
	=2R ⇒ a=8
sinα

	b
		=2R ⇒ b=5
	sinβ

	1
PABC=		*5*8*sin(α+β)=.........
	2

Eta: i znowu wredulus się wciął

Eta: Idę zobaczyć,czy nie wyskoczy z mojej lodówki

wredulus_pospolitus: Co ja miałem z lodówki wyskakiwać −−− przyszedłem, zobaczyłem co dobrego jest, zjadłem ... i poszedłem dalej

wredulus_pospolitus: @Etuś ... ja bym jednak jeszcze zapisał: sinγ = sin(180 − (α+β)) = sin(α+β) tak dla pewności co by uczeń 'załapał'

chichi: to ile wynosi to szukane pole @Michał?

Michał: @chichi Niestety dostałem zadania bez odpowiedzi.

Min. Edukacji: To nie policzyles😯❓

Michał: Przepraszam, źle przeczytałem pytanie chichi. Myślałem, że pytał o odpowiedź do zadania. Za chwilę się zabieram za to zadanie to Wam prześlę ile wyszło.

Michał: No to jedziemy z tym koksem. sinγ= sin(180°−(α+β)) = sin(α+β) = sinαcosβ + cosαsinβ sinα = 0,4 sinβ = 0,25 Potrzebuję jeszcze cosα i cosβ. Z jedynki trygonometrycznej: sin²x + cos²x = 1 cos²x = 1 − sin²x cosx = √1 − sin²x sin²α = (0,4)² = (⁴₁₀)² = ¹⁶₁₀₀ = ⁴₂₅ sin²β = (0,25)² = (²⁵₁₀₀)² = (¹₄)² = ¹₁₆

	√21		√21
cosα = √1 − sin2α = √1 − 425 = √2125 =		=
	√25		5

	√15		√15
cosβ = √1 − sin2β = √1 − 116 = √1516 =		=
	√16		4

	4		√15		√21		1
sinγ = sin(α+β) = sinαcosβ + cosαsinβ =		*		+		*		=
	10		4		5		4

	4√15		√21		2√15		√21		2√15 + √21
=		+		=		+		=
	40		20		20		20		20

	2√15 + √21
PABC = 12 * 8 * 5 * sinγ = 20 * sinγ = 20 *		= 2√15 + √21
	20

Dzięki Wszystkim za pomoc. Kocham Was.

an: Można też tak: a i b jw. następnie wysokość na c, z sinusa h_c=2 i z Pitagorasa c=c₁+c₂=√5²− 2²+√8²−2²=√21 +2√15

	c*hc
P=		=√21 +2√15
	2

chichi: nie wiem dlaczego wszyscy moi przedmówcy zakładają o ostrości kąta leżącego naprzeciwko boku o długości 8? Z jasnych przyczyn nie rozewrze nam się kąt naprzeciwko boku długości 5 gdyż 8 > 5. Drugi wariant szukanego pola to P = 2√15 − √21

Kacper: