Oblicz pole Paluszek: Oblicz pole czworokąta o bokach 1,2,3,4, jeżeli miara kąta między dwoma najkrótszymi bokami wynosi 120°

wredulus_pospolitus: ehhh ... jeżeli bardzo potrzebujemy skorzystać z tego kąta (bo nie musimy) to: 1. z tw. cosinusów wyznaczamy długość przekątnej. 2. znając długość przekątnej wyznaczamy (z tw. cosinusów) jeden z kątów trójkąta powstały z tej przekątnej i dwóch pozostałych boków. 3. korzystamy ze wzoru na pole trójkąta z wykorzystaniem sinusa kąta pomiędzy znanymi nam dwoma długościami boków (dla każdego z tych dwóch trójkątów). I gotowe

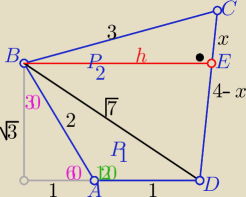
aa: Inny sposób |BD|=√7

	√3		1
P1=		P2=		*4*h = 2h
	2		2

dwa razy tw. Pitagorasa w ΔBEC i DEB h²= 7−(4−x)² i h²= 9−x² x=... h=.... P₂=... P=P₁+P₂

Mila:

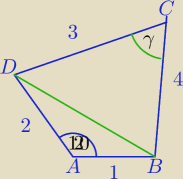
	1*2*sin120o		√3
1) [ABC]=		=
	2		2

2) |DB|²=7 3) 7=3²+4²−2*3*4*cosγ

	18		3
cosγ=		=
	24		4

sinγ=√1−9/16

	√7
sinγ=
	4

4)

	3*4		√7
[DBC]=		*
	2		4

	√3+3√7
PABCD=
	2