Wykaż Paluszek: Dany jest trójkąt ostrokątny ABC o bokach długości a,b,c i kątach leżących naprzeciw nich α,β,γ Wykaż, że b²+c²−a²/a²+c²−b² = tgβ/tgα

wredulus_pospolitus: NA WIA SY

Paluszek:

b2+c2−a2
a2+c2−b2

chichi:

	a		b		sinβ		b
tw. sinusów:		=		⇒		=
	sinα		sinβ		sinα		a

	b2 + c2 − a2		a2 + c2 − b2
z tw. cosinusów: cosα =		, cosβ =
	2bc		2ac

	tanβ		sinβ	cosα
mamy, że		=			= ... dokończ
	tanα		cosα	sinβ

chichi:

	tanβ		sinβ	cosα
wkradł się chochlik:		=
	tanα		sinα	cosβ

wredulus_pospolitus:

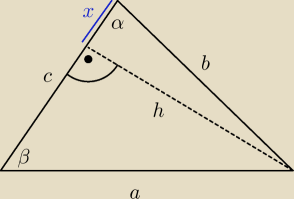
	h
tgα =
	x

	h
tgβ =
	c−x

tgβ		x		c
	=		=		− 1
tgα		c−x		c−x

z tw. Pitagorasa: b² + x² = h² = a² + (c−x)² x² − (c−x)² = a² − b² (x − c + x)(x + c − x) = a² − b² (2x−c)*c = a² − b²

	a2 − b2
2x =		+ c
	c

	a2 + c2 − b2
x =
	2c

więc:

c		2c2		2c2
	− 1 =		− 1 =		− 1 =
c−x		2c2 − (a2+c2−b2)		−a2 + b2 + c2

	a2 − b2 + c2
=		czyli odwrotność tego co Ty napisałeś.
	−a2 + b2 + c2

Sprawdź czy poprawnie przepisałeś ... jeżeli nie ... to szukaj błędu u mnie

mati:

chichi: @wredulus z mojego sposobu wychodzi teza