Pitagoras.. Kasia: Ratunku! Nie mogę tego wyliczyć, powinno wyjść x = 3..

	a − x)
(a − x)2 = x2 + (		)2
	2

gdzie: a = 2√3 + 3 Liczę i liczę i zawsze gdzieś się gubię...

Godzio: pomoge

Godzio:

	a−x
(a−x)2 = x2 + (		)2
	2

	a2−2ax + x2
a2 − 2ax + x2 = x2 +
	4

4a² − 8ax = a² − 2ax + x² 0 = −3a² + 6ax + x² Dobrze jest napisany przykład ? bo dosyć kosmiczne liczby wyjdą?

Kasia: Właśnie to samo mi wyszło... hm to może ja przepisze wcześniejszą część zadania bo to sama końcówka, wydaje sie być dobrze..

Godzio: tak myślałem że coś wcześniej jest bo nie możliwe żeby coś takiego wyszło

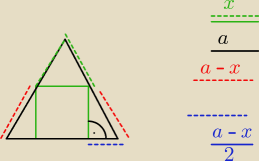
Kasia: Znajdź długość boku kwadratu wpisanego w trójkąt równoboczny o boku a = 2√3 + 2. Prawie wyszedł. I stąd wzięłam tamto równanie...

Kasia: a = 2√3 + 3 nie +2

Godzio: coś przekombinowałaś zaraz narysuje

Eta:

a		a√32
	=
x		a√32−x

otrzymasz: a(a√3−2x)= ax√3 /:a a√3−2x = x√3 x( √3+2) =a√3= √3(2√3+3)= 6+3√3= 3( 2+√3)

	3(2+√3)
x=		= 3
	2+√3

odp; x =3

Godzio:

	a√3		6 + 3√3
h =		=
	2		2

h		x
	=
1   a 2		a−x   2

	a−x		ax
h *		=		/*2
	2		2

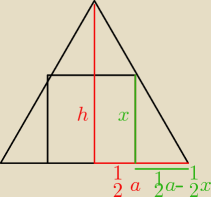
h(a−x) = ax

6 + 3√3
	(2√3+3 −x) = (2√3+3)x /*2
2

(6+3√3)(2√3+3−x) = (4√3+6)x 12√3 + 18 − 6x + 18 + 9√3 − 3√3x = 4√3x + 6x 21√3 + 36 = 7√3x + 12x 21√3 − 7√3x + 36 − 12x = 0 7√3(3−x) + 12(3−x) = 0 (3−x)(7√3+12) = 0 3−x = 0 x = 3

Eta:

Kasia: no tak bez Pitagorasa też się da.. zaraz sie odnajdę w tym. Dzięki wielkie!

Godzio: to ja się tu męczę a tu tak prosto można było

Kasia: Godzio, Twoje wymęczone rozwiązanie bardziej do mnie przemawia..