Geometria Analityczna - zadanie z testu poziomującego CKE sasito: Punkty A(2,1) B(5,−2) C(11,m) gdzie m jest dodatnią liczbą rzeczywistą są wierzchołkami trójkąta o polu równym 21. Na boku AC tego trójkąta zaznaczono punkt P, który jest równoodlegly od punktu A i B. Oblicz współrzędne punktu P

wredulus_pospolitus: 1. wyznaczamy prostą k przechodzącą przez A,B. 2. obliczamy |AB| 3. wyznaczamy proste p₁, p₂ równoległe do prostej k, która jest 'odległa' od niej o |AB| 4. wyznaczamy wartości p₁(11) oraz p₂(11) <−−− masz wartość 'm' (pamiętaj, że m > 0) 5. wyznaczasz prostą l przechodzące przez A i C. 6. wyznaczasz środek odcinka AB 7. wyznaczasz prostą m prostopadłą do k, przechodzącą przez środek odcinka AB 8. wyznaczasz punkt przecięci się prostych m i l <−−− i masz współrzędne punktu P.

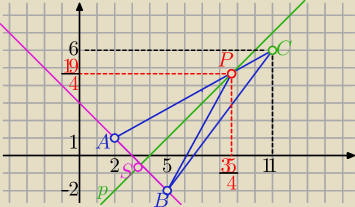
Eta: Można tak:

	1
PABC=		|AB|*h =21 gdzie h −− odległość punktu C od prostej AB
	2

|AB|=3√2 prosta AB : y= −x+3 ⇒ x+y−3=0 −− postać ogólna

	|11+m−3|		|m+8|
h=		=
	√2		√2

	1		|m+8|
to P=		*3√2*		= 21 ⇒ m= 6 bo m>0
	2		√2

C= (11,6) teraz |AP|²=|BP|² P∊ prostej AC ( obliczenia żmudne ale prowadzą do celu

	35		19
P=(		,		)
	4		4

albo tak ΔAPB równoramienny napisz równanie jego wysokości p ⊥ AB i rozwiąż układ równań prostej p z prostą AC

	35		19
P=(		,		)
	4		4

===========