prawdopodobieństwo krokodyl: z jakiego wzoru mam skorzystać aby obliczyć P(A1sumaA2sumaA3) mam odpowiedź ale nie wiem z jakiego wzoru skorzystano

.: P(AuB) = P(A) + P(B) − P(AnB) I teraz: B = A₂ u A₃ wstawiasz i znowu korzystasz + (dwa razy o ile dobrze kojarzę) z tego wzoru, plus z praw działań na zbiorach

krokodyl: a skąd się bierze A1iloczynA2iloczynA3?

.: Będzie z rozpisania P(A n (A₂ u A₃))

krokodyl: a może ktoś to całe rozpisać po kolei bo nie widzę tego?

ABC: wzór nad "Bibliografia" , wcześniejsze też możesz poczytać https://pl.wikipedia.org/wiki/Zasada_w%C5%82%C4%85cze%C5%84_i_wy%C5%82%C4%85cze%C5%84

Mila: Masz wykazać prawdziwość sumy : P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C) ?

krokodyl: i ten wzór należy zapamiętać czy z wzoru z 16:26 można wyprowadzić?

wredulus_pospolitus: oczywiście, że można ze wzoru 16:26 wyprowadzić. Tak samo jak wzór na (a+b+c)² = a² + b² + c² + 2ab + 2ac + 2bc można wyprowadzić ze wzoru (x+y)² = x² + 2xy + y²

wredulus_pospolitus: z drugiej strony ... powinien to być na tyle łatwy wzór do zapamiętania że powinieneś go kojarzyć ... 'metoda włączeń i wyłączeń" się tutaj kłania, zresztą dostałeś nawet link do wikipedii.

kerajs: Rysuj obrazki, czyli diagram Venna. To wystarczy.

Mila: Masz wyprowadzić: P(A∪B)=P(A)+P(B)−P(A∩B) masz udowodnione ? P(A∪B∪C)=P( (A∪B)+C)=P(A∪B)+P(C)−P((A∪B)∩C)= =P(A)+P(B)−P(A∩B) +P(C)− P((A∩C)∪(B∩C))= =P(A)+P(B)+P(C)−P(A∩B)−[P(A∩C)+P(B∩C))−P(A∩C∩B∩C)]= =P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C))+P(A∩B∩C)

krokodyl: dziękuję

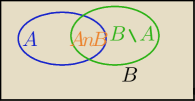
Mila: P(A∪B)=?P(A)+P(B)−P(A∩B) Patrz na diagram: 1) P(A∪B)=P(A)+P(B\A) 2) P(B)=P(A∩B)+P(B\A) P(B\A)=P(B)−P(A∩B) 3) Podstawiając do (1) P(A∪B)=P(A)+P(B\A)=P(A)+P(B)−P(A∩B)