Zadania z geometrii AAr: 1.Punkt G leży na boku BC kwadratu ABCD. Punkty E i F leżą na zewnątrz kwadratu ABCD i są wierzchołkami kwadratu BEFG (punkt B leży na odcinku AE). Wyznaczanie długośc odcinka FD. 2. W trójkącie prostokątnym o kącie prostym przy wierzchołku C i kącie ostrym przy wierzchołku A rownym 30° długość przeciwprostokątnej jest równa 12. Środek okręgu stycznego do boków AC i BC tego trójkąta leży na przeciwprostokątnej. Wyznacz długość promienia tego okręgu. Prosze o podpowiedzi, nie rozwiazania

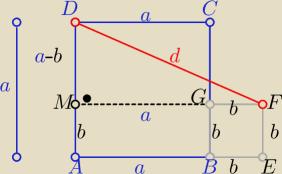
CCr: a>b |MB|=a+b, |MD|=a−b 1) zastosuj tw. Pitagorasa w ΔDMF d=..............

galanonim: zapomnialem dodac, w 1 zadaniu mamy podane AG = 5

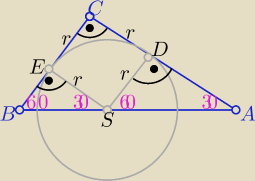
CCr: |AB|=12 to |BC|=6 i |AC|=6√3 ( myślę,że to wiesz to |AD|= 6√3−r r∊(0,6√3) skorzystaj z podobieństwa trójkątów ABC i ASD

	r		6√3−r
		=
	6		6√3

r=.......

CCr: No to w zad 1 |AG|= 5 to |AG|²=a²+b²=25 i otrzymasz ...... |DF|=50

CCr: i otrzymasz ..... |DF|²=50 |DF|= 5√2