prawdopodobienstwo unia: prawdopodobieństwo warunkowe a wzor bayesa czy ktos umie na chlopski rozum pokazac roznice bo dla mnie oba mowia o zajsciu czegos pod warunkiem innego warunku

Qulka: to to samo tylko w Bayesie warunkiem jest pr−wo całkowite

wredulus_pospolitus: Bo tak dokładnie jest. Wzór Bayesa pomaga nam w obliczeniu prawdopodobieństwa warunkowego w momencie gdy łatwiej jest policzyć 'odwrotne' prawdopodobieństwo warunkowe. O co mi chodzi. Mamy takie zadanie. Mamy dwie urny. W urnie nr 1 mam 5 kul białych i 5 kul czarnych, w urnie nr 2 mamy 3 kule białe i 7 kul czarnych. Losujemy z losowo wybranej urny dwie kule i przerzucamy je do drugiej urny, następnie losujemy jedną kulę z drugiej urny i dajemy ją Zosi. Oblicz prawdopodobieństwo, że najpierw losowaliśmy z urny 1 pod warunkiem, że Zosia dostała kulę czarną. Gdybyśmy tutaj chcieli wyznaczyć to prawdopodobieństwo warunkowe 'wprost' to oczywiście, byłoby to możliwe, ale trochę musielibyśmy się napocić. Jednak o wiele łatwiej będzie nam policzyć prawdopodobieństwo wylosowania czarnej pod warunkiem, że najpierw losujemy z urny 1 i stosując wzór Bayesa, dojść do tego pierwotnego 'problemu'. Ja osobiście nigdy nie korzystałem ze wzoru Bayesa, tylko wyliczałem wprost ... ale to ja.

unia: nie bardzo wiem jaka to jest roznica oba zakladaja ze cos sie wydarzylo w przeszlosci i wobec tego kieruje nam to sciezke prawdopodobiensdtwa dla 2 przypadku

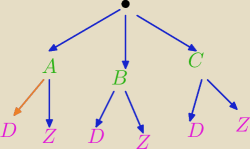
Qulka: prawdopodobieństwo warunkowe np że D pod warunkiem że z A (pomarańczowa strzałka) P(D|A) = P(D|A)•P(A) / P(A) prawdopodobieństwo całkowite że D P(D)=P(D|A)•P(A)+P(D|B)•P(B)+P(D|C)•P(C) prawdopodobieństwo warunkowe np że A pod warunkiem że D (używamy Bayesa bo musimy uwzględnić całkowite) P(A|D)= P(D|A)•P(A) / P(D)