sp19 konkurs dla 8 klas
świruś:
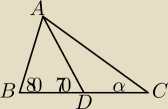
Miara zaznaczonego kąta na rysunku pomocniczym, jeśli AC=AB+BD wynosi:
A. 10 stopni
B. 20 stopni
C. 30 stopni
D. 40 stopni
podobno prawidłowa odpowiedź to D
6 mar 19:14
Świrus : Wredulus pomóż
6 mar 20:18
Świrus : Mi wychodzi 10 stopni:(
6 mar 20:23
Świrus : Albo nie
6 mar 20:27
Świrus : Nic mi nie wychodzi
6 mar 20:27
wredulus_pospolitus:
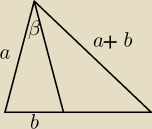
β = 180 − 80 − 70 = 30
| | a | |
r1 = |
| ; r1 −> promień okręgu opisanego na ABD |
| | 2sin70o | |
−−−>
| | 2sin70o + 1 | |
a+b = a( |
| ) |
| | 2sin70o | |
| | a+b | |
R2 = |
| ; R2 −> promień okręgu opisanego na ABC |
| | 2sin80o | |
−−−>
| | 2sin70osin80o | | 2sin70osin80o | |
sinα = |
| = |
| = |
| | 2sin70o + 1 | | 2(sin70o + sin30o) | |
| | sin70osin80o | | sin70osin80o | |
= |
| = |
| = |
| | 2sin50ocos20o | | 2sin50osin70o | |
| | sin80o | | sin80o | | sin80osin40o | |
= |
| = |
| = |
| = |
| | 2sin50o | | 2cos40o | | 2cos40osin40o | |
| | sin80osin40o | |
= |
| = sin40o |
| | sin80o | |
trooochę zabawy z przekształceniami ... nie wiem czy wszystkie te wzory były na poziomie 8
klasy podstawówki (no ale niby to konkursowe zadanie).
Możliwe, że da się to jakimś ciekawym twierdzeniem załatwić, ale nie jestem specjalistą w
planimetrii.
6 mar 20:38
wredulus_pospolitus:
wykorzystane wzory:
| | a | |
1. tw. sinusów (r = |
| ) |
| | 2sinα | |
2. sinα = cos(90 − α)
| | α+β | | α−β | |
3. sinα + sinβ = 2sin |
| cos |
| |
| | 2 | | 2 | |
4. sin(2α) = 2sinαcosα
nie wiem czy wzór (3) jest Ci znany.
6 mar 20:44
świruś: miałam sobie z tym poradzić bez trygonometrii
6 mar 20:45
świruś: :(
6 mar 20:46
wredulus_pospolitus:
no nie wiem ... może się da bez trygonometrii

może jakoś się da wyłuskać, że AD jest
dwusieczną ... nie wiem ... jak wspomniałem − specjalistą od planimetrii nie jestem, była to
moja 'kula u nogi' już za czasów podstawówki.
6 mar 20:47
chichi:
narzuca się proste syntetyczne rozwiązanie, poczekam jeszcze trochę może wpadniesz na
rozwiązanie, jeśli nie to napisz i wrzucę

6 mar 20:51
świruś: napisz proszę
6 mar 20:53
chichi:
konkursowiczom nie wypada bez dłuższej walki prosić o rozwiązanie

6 mar 21:09
świruś: skąd wiesz ile czasu próbowałam?
6 mar 21:14
chichi:
dzisiaj był konkurs, więc zdecydowanie za mało próbowałaś XD
6 mar 21:18
świruś: Co Ci szkodzi przedstawić rozwiązanie? Może chcę po prostu zobaczyć jak ktoś inny rozwiązuje

6 mar 21:21
świruś: To napisz wskazówkę, jeśli nie masz pełnego rozwiązania
6 mar 21:22
świruś: 327+329 udowodnij podzielność przez 30
a to?
z tego samego konkursu
6 mar 21:29
chichi:
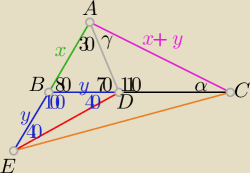
odkładam odcinek długości 'y' wzdłuż boku AB, ΔEBD − równoramienny, |∡EDA| = 110
o = |∡ADC|
zatem D leży na wysokości ΔAEC (równoramienny), stąd γ = 30
o, a zatem α = 40
o 
6 mar 21:33
wredulus_pospolitus:
na pewno przez 30 a nie przez 10

bądź 20 bądź 40

6 mar 21:35
ABC: jakiś troll,
327+329= 327(1+1024)=235*52*41 nie dzieli się przez 30 bo nie dzieli się przez 3
6 mar 21:37
chichi:
327 + 329 nie dzieli się przez 30.
6 mar 21:37
świruś: jak to wywnioskowałeś, że D leży na wysokości?
6 mar 21:46
świruś: no takie jest polecenie
i nie umiałam wykazać
6 mar 21:49
wredulus_pospolitus:
tak naprawdę wystarczy zauważyć, że ADE podobny do ADC (podobieństwo bbk)
6 mar 21:55
ABC:
jest gdzieś w sieci oryginalny arkusz z tego konkursu?
6 mar 21:56
chichi:
też bym zerknął, bo wątpię, że takiego bubla by strzelili na konkursie

6 mar 22:05
świruś: serio
6 mar 22:06
świruś: może jakiś błędny arkusz dostałam, ale wątpię:(
jak mi się uda zeskanować to wrzucę
6 mar 22:13
6 mar 22:43
świruś: zadanie nr 3
6 mar 22:43
ABC:
to ktoś układający się nie popisał , a może specjalnie sabotaż bo kazali mu za darmo to robić

6 mar 22:47
świruś: a ja za Chiny ludowe nie mogłam tego udowodnić:(
6 mar 22:49
 Miara zaznaczonego kąta na rysunku pomocniczym, jeśli AC=AB+BD wynosi:
A. 10 stopni
B. 20 stopni
C. 30 stopni
D. 40 stopni
podobno prawidłowa odpowiedź to D
Miara zaznaczonego kąta na rysunku pomocniczym, jeśli AC=AB+BD wynosi:
A. 10 stopni
B. 20 stopni
C. 30 stopni
D. 40 stopni
podobno prawidłowa odpowiedź to D
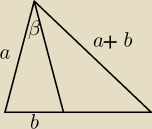 β = 180 − 80 − 70 = 30
β = 180 − 80 − 70 = 30
 może jakoś się da wyłuskać, że AD jest
dwusieczną ... nie wiem ... jak wspomniałem − specjalistą od planimetrii nie jestem, była to
moja 'kula u nogi' już za czasów podstawówki.
może jakoś się da wyłuskać, że AD jest
dwusieczną ... nie wiem ... jak wspomniałem − specjalistą od planimetrii nie jestem, była to
moja 'kula u nogi' już za czasów podstawówki.



 odkładam odcinek długości 'y' wzdłuż boku AB, ΔEBD − równoramienny, |∡EDA| = 110o = |∡ADC|
zatem D leży na wysokości ΔAEC (równoramienny), stąd γ = 30o, a zatem α = 40o
odkładam odcinek długości 'y' wzdłuż boku AB, ΔEBD − równoramienny, |∡EDA| = 110o = |∡ADC|
zatem D leży na wysokości ΔAEC (równoramienny), stąd γ = 30o, a zatem α = 40o 
 bądź 20 bądź 40
bądź 20 bądź 40 

