kwadrat
matura:
Dany jest kwadrat ABCD o boku długości 3.
Punkty K i L leżą na prostych
odpowiednio AB i BC tak,że |BK|=2√3 i |BL|=2
Odcinek KL przecina przekątną BD w punkcie M
Wykaz,że | MD|=√6
2 mar 22:30
wredulus_pospolitus:
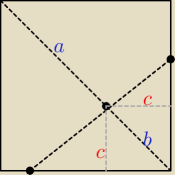
| | 1 | | 1 | |
PΔKBL = PΔKBO + PΔLBO = |
| 2*c + |
| 2√3*c = c(1 + √3) |
| | 2 | | 2 | |
| | 2√3 | |
stąd: c = |
| = √3(√3−1) = 3 − √3 |
| | √3+1 | |
stąd: b = (3−
√3)*
√2 = 3
√2 −
√6
|BD| = a + b −−−> 3
√2 = a + (3
√2 −
√6) −−−> a =
√6
c.n.w.
2 mar 23:14
Eta:
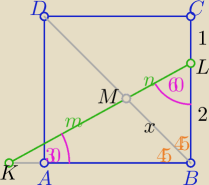
Z treści zadania wynika,że ΔKBL jest "ekierkowy"o kątach 30
o,60
o,90
o
to |KL|=4
| | m | | 2√3 | |
z tw. odwusiecznej w ΔKBL |
| = |
| = √3 to m= n√3 |
| | n | | 2 | |
m+n=4 ⇒ n=(
√3+1)=4 ⇒ n= 2(
√3−1)
z tw. sinusów w ΔBLM
x= 3
√2−
√6
i |BD|=3
√2
to |MD|= |BD|−x
|MD|=
√6
==========
c.n.w.
2 mar 23:17
wredulus_pospolitus:
faktycznie |KB| > |AB|

więc mój rysunek do poprawy ... jednak samo rozwiązanie pozostaje
bez zmian
2 mar 23:20
Eta:

2 mar 23:21
wredulus_pospolitus:
swoją drogą ... ciekawe czy gdyby to zadanie było na maturze, to obcięliby punkt za
nieprawidłowy rysunek
2 mar 23:23
wredulus_pospolitus:
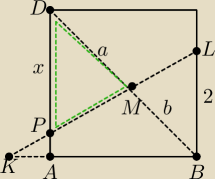
ale wtedy 'na dokładkę' trzeci sposób podam
ΔKAP podobny do ΔKBL (podobieństwo kkk) lub z tw. Talesa.
| |AP| | | 2 | |
| = |
| oraz wiemy, że |AK| = 2√3 − 3 |
| |AK| | | 2√3 | |
stąd |DP| = x = 3 − (2 −
√3) = 1 +
√3
ΔLBM (
zielony trójkąt) podobny do ΔPDM (podobieństwo kkk)
| a | | b | | 2 | | 2 | |
| = |
| −−> b = a* |
| = a* |
| = a(√3−1) |
| x | | 2 | | x | | √3+1 | |
a wiemy, że |BD| = 3
√2 = a + b −−−> 3
√2 = a + a(
√3−1) = a
√3
2 mar 23:36
Mila:
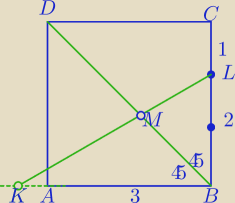
|KB|=2
√3>3
1)
|DB|=3
√2
|DM|=
√6 ?
==========
2)
=========== − długość odcinka dwusiecznej kąta prostego
w Δ prostokątnym o przyprostokątnych a i b
| | 2√3*2*√2 | |
|BM|= |
| =3√2−√6 |
| | 2√3+2 | |
|MD|=
√6
3 mar 00:31

 Z treści zadania wynika,że ΔKBL jest "ekierkowy"o kątach 30o,60o,90o
to |KL|=4
Z treści zadania wynika,że ΔKBL jest "ekierkowy"o kątach 30o,60o,90o
to |KL|=4
 więc mój rysunek do poprawy ... jednak samo rozwiązanie pozostaje
bez zmian
więc mój rysunek do poprawy ... jednak samo rozwiązanie pozostaje
bez zmian

 ale wtedy 'na dokładkę' trzeci sposób podam
ΔKAP podobny do ΔKBL (podobieństwo kkk) lub z tw. Talesa.
ale wtedy 'na dokładkę' trzeci sposób podam
ΔKAP podobny do ΔKBL (podobieństwo kkk) lub z tw. Talesa.
 |KB|=2√3>3
1)
|DB|=3√2
|DM|=√6 ?
==========
2)
|KB|=2√3>3
1)
|DB|=3√2
|DM|=√6 ?
==========
2)