proszę o rozwiązanie anna: punkty A(0 ; −2 ) i B = (4 ; 6 ) są wierzchołkami trójkąta prostokątnego ABC którego przeciwprostokątna AC jest zawarta w osi y Wyznacz równanie okręgu opisanego na tym trójkącie

Jolanta: Narysuj ten trójkąt to zobaczysz,że na osi y jest przyprostokatna przy wierzchołku C jest kat prosty Gdzie znajduje się środek okręgu opisanego na trójkącie prostokątnym? Jaki jest wzór na okrag? Jaki jest wzór na obliczenie środka odcinka? Środek odcinka AB to środek okregu

.: Jolanta − przy wierzchołki B masz kąt prosty.

.: Sposób nr 1. Bez wyznaczania współrzędnych punktu C. Wzór okręgu: x² + (y − a)² = r² gdzie ośrodek okręgu ma współrzędne (0,a) Podstawiasz współrzędne wierzchołka A, wstawiasz współrzędne wierzchołka B Uzyskujesz w ten sposób układ dwóch równań z dwoma (a i r) niewiadomymi. Rozwiazujesz i po sprawie

Jolanta: Jeżeli chcesz się nauczyć to zrób rysunek Bardzo to pomaga (x−a)²+(y−b)²=r² a i b to współrzędne środka okręgu S(a,b) Środek okręgu jest srodkiem przeciwprostokątnej AB Połowa tej przeciwprostokątnej to promień r Policzymy długość AB |AB|=√(x_B−x_A)²+(y_B−y_A)²=√(4−0)²+(6+2)²=√16+64=√80=4√5 r=1/2*4√5=2√5 Teraz środek

	xA+xB		0+4
xsr=		=		=2
	2		2

	yA+yB		−2+6
ysr=		=		=2
	2		2

S(2,2) (x−2)²+(y−2)²=(2√5)² (x−2)²+(y−2)²=20

Jolanta: Kurcze ,myślałam,że literówkę zrobila

anna: przepraszam ale przeciwprostokątna trójkąta ABC to AC a nie AB

anna: dziękuję za wskazówki ^._.. 1 mar 18:16 Wynik to x² + (y − 4 )² = 36 S =(0; 4 ) − Środek okręgu r = 6

anna: pomyłka x² + ( y−3)² = 25 b = 3 r = 5

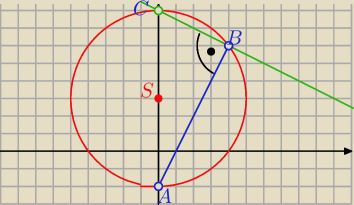
Eta: można też tak: pr. AC ⊥ pr. AB

	8
aAB=		=2 aBC= −1/2
	4

	1		1
to AC : y= −		(x− 4)+6 ⇒ AC : y = −		x+8 ⇒ C=(0,8)
	2		2

to S jest środkiem odcinka AC S=(0,3) i r= |AS|=5 o: x²+(y−3)²=25 ==============

Eta: poprawiam zapis pr. CB⊥ pr. AB i dalej

	1
CB : ..... CB : y=−		x+8 ⇒ C=(0,8)
	2