Oblicz współrzędne punktów wspólnych prostej
Ada: Oblicz współrzędne punktów wspólnych prostej o równaniu y = x + 2
i okręgu o środku w punktach S = (−3, 2) i promieniu długości 3.
29 lut 08:14
Jolanta: Znasz wzór na okrag?
29 lut 13:18
Ida:
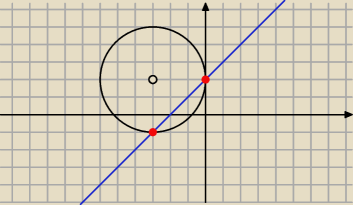
29 lut 19:27
Bai Xue:
y=x+2
(x+3)2+(y−2)2=9
(x+3)2+(x+2−2)2=9
2x2+6x+9=9
2x2+6x=0
2x(x+3)=0
x=0 lub x=−3
x=0 to y=2
x=−3 to y=−1
Liczone w pamięci więc sprawdz jeszcze raz obliczenia
29 lut 21:20
wredulus_pospolitus:
alternatywna wersja:
l: y = x+2, S = (−3, 2)
1. prostopadła do l przechodząca przez S:
y = −x + b −−−> 2 = 3 + b −−−> b = −1 −−−> k: y = −x −1
2. przecięcie prostych l i k:
−x − 1 = x+2 −−−> x = −1.5 −−−> y = 0.5 −> O = (−1.5 , 0.5) punkt przecięcia
3. odległość punktu S od prostej l (można z gotowego wzoru bądź ze wzoru na długość odcinka
mając współrzędne punktów S i O) = 1.5√2
4. z tw. pitagorasa:
32 = (1.5√2)2 + a2 −−−> a2 = 4.5 −−−> a = 1.5√2
5. odkładamy taką odległość na prostej l (od punktu O) i mamy punkty o współrzędnych (−3, −1)
oraz (0 , 2)
29 lut 21:27
