Stereometria Paweł: W stożek o promieniu podstawy 6 wpisano graniastosłup prawidłowy czworokątny. Przekątna graniastosłupa ma długość 2√13 , a pole jego podstawy jest równe 18. Oblicz objętość stożka. Wiemy, że promień to połowa przekątnej kwadratu czyli 3√2 / 2 Wiemy też, że wysokość graniastosłupa to 34 cm. Jak obliczyć wysokość stożka?

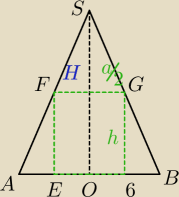
ite: H − wysokość stożka h − wysokość graniastosłupa a − bok podstawy graniastosłupa podpowiedź na rysunku: skorzystaj z podobieństwa trójkątów powstających z tego przekroju

Paweł: proporcja ? x/ 3{p}2/2 = x + 34 / 3√2

ite: teraz zauważyłam pomyłkę: d − przekątna kwadratu |FG| = d/2

ite: obracając model https://www.geogebra.org/3d/rxz3vrqm sprawdź, czy tak jak piszesz "promień (stożka?) to połowa przekątnej kwadratu"

Paweł: czyli 1/4 przekątnej?

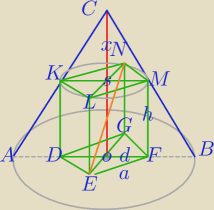
Mila: |EN|=2√13,|OB|=R=6 1) a²=18⇔ a=3√2 |DF|=|EG|=6 d=3 2) W ΔEGN: h²+6²=(2√13)² h²=52−36, h=√16, h=4 3)ΔCSM∼ΔCOB :

x		x+4
	=
3		6

x=4 H=|OC|=8

	1
4) Vs=		π*62*8
	3

Mila: Wysokość graniastosłupa nie może być równa 34 bo 34>2√13.