Rachunek Prawdopodobieństwa - Studia H: Rozważmy wektor losowy (X,Y) o rozkładzie zadanym gęstością g(x,y)=x/a1_D(x,y), gdzie D jest trójkątem o wierzchołkach (0,0) (2,0) (0,−1) zaś a>0 jest pewną stałą. a) wyznacz a b) Oblicz P(x − 1/2 ≤ y) c) Wyznacz E(Y − X|X) Proszę o pomoc z podpunktem b, zwłaszcza z wyznaczeniem granic całkowania. Zrobiłem podwójną całkę od 0 i x−1/2 dla dy i od 1/2 do 0 dla dx, ale nie wiem czy jest to poprawne. Jeśli chodzi o a) to parametr a wyszedł mi 2/3. W podpunkcie c mam zamiar wyliczyć E(Y|X) z całki y(g(x,y)/g(x)). Prosiłbym o potwierdzenie czy jest to poprawne podejście.

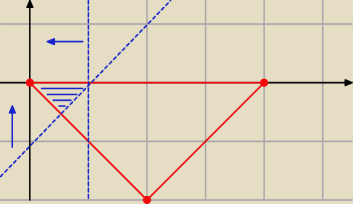
wredulus_pospolitus: zaznaczyłem Ci obszar całkowania trójkącik o wierzchołkach (0,0) , (1/2,0), (1/4, − 1/4)