
 Zakładam, że jest to sześcian FORMENY
Zakładam, że jest to sześcian FORMENY  Możesz na parę sposobów do tego podejść.
Podejście nr 1.
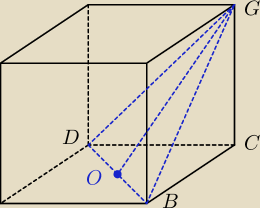
1. Patrz rysunek.
2. Wyznaczamy |OC| (połowa przekątnej podstawy), znamy |CG|.
3. Liczymy pole trójkąta OCG.
4. z tw. Pitagorasa wyznaczamy |OG|.
5. Mamy pole trójkąta OCG ... teraz OG traktujemy jako podstawę tegoż trójkąta ... wyznaczamy
wysokość odpuszczoną z wierzchołka C.
To jest szukana odległość
Możesz na parę sposobów do tego podejść.
Podejście nr 1.
1. Patrz rysunek.
2. Wyznaczamy |OC| (połowa przekątnej podstawy), znamy |CG|.
3. Liczymy pole trójkąta OCG.
4. z tw. Pitagorasa wyznaczamy |OG|.
5. Mamy pole trójkąta OCG ... teraz OG traktujemy jako podstawę tegoż trójkąta ... wyznaczamy
wysokość odpuszczoną z wierzchołka C.
To jest szukana odległość
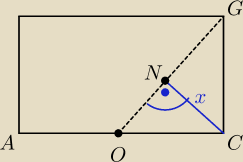 Podejście nr 3
bierzemy pod uwagę płaszczyznę przechodzącą przez ACG.
Zauważ podobieństwo trójkątów OCG i ONC (podobieństwo KKK)
Podejście nr 3
bierzemy pod uwagę płaszczyznę przechodzącą przez ACG.
Zauważ podobieństwo trójkątów OCG i ONC (podobieństwo KKK)

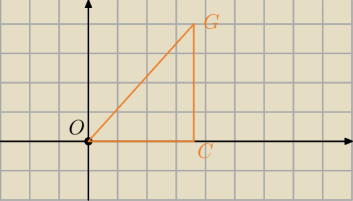 Może jeszcze podejście nr 4.
Geometria analityczna.
Może jeszcze podejście nr 4.
Geometria analityczna.
| √2 | ||
wyznacza wzór prostej f(x) przechodzącej przez punkty O(0,0) i G( | a , a). | |
| 2 |
| √2 | ||
wyznaczasz odległość punktu C( | a , 0) od prostej f(x). | |
| 2 |
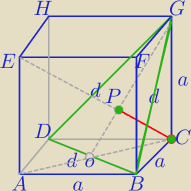 Możesz to obliczyć sam?
Masz co najmniej 3 sposoby.
Możesz to obliczyć sam?
Masz co najmniej 3 sposoby.
| 1 | √2a | a2√2 | ||||
PΔCOG= | * | *a= | ||||
| 2 | 2 | 4 |
| a√2*√3 | ||
|OG|= | ||
| 2 |
| 1 | ||
PΔCOG= | |OG|*h | |
| 2 |
| a√2*√3 | ||
PΔCOG= | *h | |
| 4 |
| a√2*√3 | a2√2 | ||
*h= | |||
| 4 | 4 |
| a | √3a | |||
h= | = | |||
| √3 | 3 |
| 1 | a2 | a3 | ||||
VDBCG= | * | *a= | ||||
| 3 | 2 | 6 |
| √3 | a2√3 | |||
PΔDBG= | *(a√2)2= | |||
| 4 | 2 |
| 1 | a2√3 | a2√3 | ||||
VDBCG= | * | *|PC|= | *|PC| | |||
| 3 | 2 | 6 |
| a2√3 | a3 | ||
*|PC|= | |||
| 6 | 6 |
| a | √3 | |||
|PC|= | = | |||
| √3 | 3 |
| √3a | ||
|PC|= | ||
| 3 |
