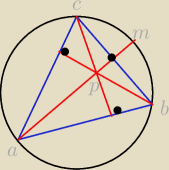
Dany jest trójkąt ostrokątny ABC, którego wysokości przecinają się w punkcie P prosta AP
przecina okrąg opisany na tym trójkącie w punkcie M (zobacz rysunek poniżej)
Wykaż, że lBMl = lBPl
PS zakropkowane miejsca to kąt prosty
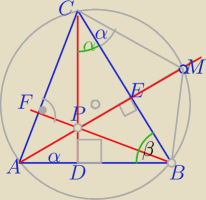1)
∡MAB=∡MCB=α − jako kąty wpisane oparte na tym samym łuku.
2)
ΔAEB i ΔCDB − Δprostokątne , mają wspólny kąt przy wierzchołku B⇒są podobne
∡DCB=α⇒|PE|=|EM|
3) ΔPEB ≡ ΔBEM cecha kbk⇒
|BP|=|BM|