Czworościan jacek12: Odrębnym aspektem, ale nie mniej ważnym są przekroje jakie można otrzymać przecinając czworościan foremny płaszczyznami. Sytuacje te ilustruje poniższy pokaz slajdów. Kiedy czworościan foremny ustawimy tak, że podstawą jest jedna z jego ścian, to przekrój płaszczyzną równoległą do podstawy da nam zawsze trójkąt podobny do tej podstawy. Czy figura, która powstawała na skutek tego przekroju jest również czworościanem foremnym? Jeśli tak, to dlaczego?

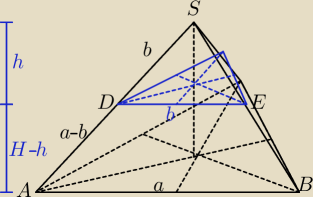
wredulus_pospolitus: tak .... patrz podobieństwa trójkątów

	b
1. Otrzymujemy trójkąt podobny (niebieski) stąd mamy proporcję
	a

2. w trójkącie ABS mamy odcinek DE który jest równoległy do podstawy AB ... podobieństwo

	|DS|
trójkątów lub jak wolisz tw. Talesa wchodzi tutaj do gry i mamy proporcję		=
	|AB|

	|DE|
	|AB|

3. związku z tym ... mamy czworościan foremny o boku 'b' (i wysokości h)