dowod :DDD: Wykaż, że jeśli długości a, b, c boków trójkąta spełniają równość 1/𝑎+𝑏 +1/𝑏+𝑐 =3/𝑎+𝑏+𝑐, to promień okręgu opisanego na tym trójkącie jest równy √3/3𝑏.

ABC: czytelnik łatwo zauważy (czytaj po żmudnych acz wykonalnych rachunkach otrzymujemy) że ten warunek z założenia jest równoważny b²=a²+c²−ac czytelnik porówna to z tw.cosinusów , otrzymując cosβ=1/2 a następnie zastosuje tw.sinusów Pij kakao, przekształcaj śmiało

www: https://zadania.info/d1427/5708633

Mila: 1)

1		1		3
	+		=		/*(a+b+c)
a+b		b+c		a+b+c

a+b+c		a+b+c
	+		=3
a+b		b+c

	c		a
1+		+1+		=3
	a+b		b+c

2)

c		a
	+		=1 / *((a+b)(b+c))
a+b		b+c

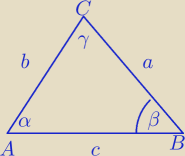
c*(b+c)+a(a+b)=ab+ac+b²+bc bc+c²+a²+ab=ab+ac+b²+bc c²+a²=ac+b² (*) b²=c²+a²−ac 3) z Tw. cosinusów b²=a²+c²−2ac cosβ i z (*) 2cosβ=1

	1
cosβ=
	2

β=60^o 4) U{b}{sin60^o)=2R Jak pisze ABC łatwe ale, żmudne