Zadanie 7 Adam : w czworokącie wypukłym ABCD dwusieczna kąta A zawiera przekątną AC oraz AB = 14, BC = 12, CD = 13 i DA = 9 oblicz cosinus największego kąta tego czworokąta

wredulus_pospolitus: fajne zadanko ... zanim podam moją propozycję rozwiązania tego zadania −−−− masz jakiś pomysł na to zadanie

Adam: Szczerze nie mam pojęcia, a te które próbowałem totalnie nie wypaliły.

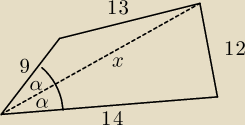
wredulus_pospolitus: cholera ... chciałem 'szprytnie' ale mi nie wyszło. Więc niestety chyba trza będzie się pomęczyć z obliczeniami. Głównie używany wzór: tw. cosinusów. 1. skorzystamy z tego, że dwusieczna zawiera się w przekątnej: 13² = 9² + x² − 18x*cosα 12² = 14² + x² − 28x*cosα wyznaczasz cosα z obu równań i przyrównujesz te równania do siebie. W ten sposób wyznaczasz 'x'. 2. Wstawiasz 'x' do jednego z równań i wyznaczasz cos(α). 3. Z trygonometrii cos(2α) = 2cos²(α) − 1 <−−− masz cosinusa jednego kąta. 4. Mając 'x' możesz wyznaczyć (z tw. cosinusów) dwóch kątów (wierzchołki B i D). 5. Co do ostatniego kąta to można poradzić sobie z tym na parę sposób. a. najpierw korzystasz z tablic aby sprawdzić czy w ogóle jest sens się tym kątem zajmować. b. możesz wyznaczyć drugą przekątną (y) i wyliczyć jej długość koszystając z tw. cosinusów i wartości cos(2α) i później wykorzystać tę wartośc do wyznaczenia cosinusa kąta przy C. c. możesz się pobawić w wyznaczanie cosinusów tych mniejszych kątów przy C (patrz rysunek) ... później wyznaczyć sinusy tychże kątów i skorzystać ze wzoru na cos(a+b) = ....

Adam : Siemka mały update, najmniejszy kąt wyszedł, −5/13, tak jak w odpowiedzi był tą kąt ABC, dzięki za pomoc

wredulus_pospolitus: to coś nie tak Ci wyszło skoro NAJMNIEJSZY kąt ma cosinusa ujemnego ... to znaczy, że jest to kąt > 90^o Kąt ABC Jesteś tego pewny? Patrząc na boki to ADC powinien być większym kątem (krótsze boki przy kącie => większy kąt w momencie gdy trójkąty mają jeden wspólny bok)

Adam: Sorki, pomyliło mi się, bo zamiast największy powiedziałem najmniejszy haha. Największy cosinus kąta −5/13