równanie z parametrem Gosia: Dla jakich wartości parametru m suma odwrotności dwóch różnych pierwiastków równania jest większa od −6 mx²+(m−1)x+1=0ał. 1⁰ a≠0 2⁰ Δ >0 3⁰

1		1
	+		<6
x1		x2

Rozw. 1⁰ m≠0 2⁰ m₁=3−2√2 m₂=3+2√2 3⁰ m>7 Odp Biorę część wspólną i nie zgadza mi się wynik Proszę o wskazanie gdzie zrobiłam błąd?

chichi:

	1		1
3o		+		> −6
	x1		x2

to raz, dwa brakuje 4ego warunku, który w tym równaniu akurat nic nowego nie wniesie 4^o x₁x₂ ≠ 0

Gosia: Dziękuje. Przy rozwiązaniu wzięłam −6 Odp. w podręczniku jest taka m∊(−∞;0)u (3−2√2)u(3+2√2;7) Z odpowiedzi wynika, że m<7

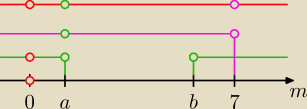
chichi: wychodzi: 1^o) m ∊ R \ {0} 2^o) m ∊ (−∞,3 − 2√2) ∪ (3 + 2√2,+∞) 3^o) m ∊ (−∞,7) 4^o) m ∊ R na rysunku: a = 3 − 2√2, b = 3 + 2√2 zatem odp. końcowa, to: m ∊ (−∞,0) ∪ (0,3−2√2) ∪ (3+2√2,7)

Gosia: Bardzo dziękuję, czyli mam błąd w 3⁰

Gosia: Bardzo ładne rozwiązanie, jeszcze raz dziękuję