Oblicz długść promienia okręgu opisanego Preppers: W trójkącie ABC kąt A ma miarę 120 stopni oraz BO = 6 i CO = 2√3 gdzie O jest środkiem okręgu wpisanego w trójkąt ABC. Oblicz długość promienia opisanego na tym trójkącie.

Saizou :

	√7
mi wyszło R=
	8

Preppers : powinno być 2√7 . jaki miałeś pomysł na to zadanie bo ja, żeby obliczyć miarę kąta BOC i zastosować twierdzenie cosinusów w trójkącie BOC, ale nie wiem jak sie za to zabrać

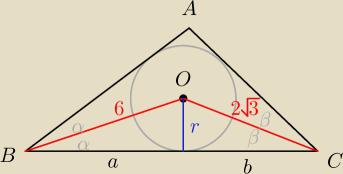
Saizou : 180 = 120 + 2α +2β → β = 30−α

	r
sinα =		→ r = 6sinα
	6

	r
sin β =		→ r = 2√3sinβ
	2√3

6sinα = 2√3sinβ 6sinα = 2√3sin(30−α)

	1		√3
6sinα = 2√3(		cosα−		sinα)
	2		2

6sinα = √3cosα − 3sinα 9sinα = √3cosα

	√3
tgα =		→ a = x√3 oraz r = 9x
	9

z tw. Pitagorasa 36 = 3x²+81x² 84x² = 36

	36		9		3		21
x2 =		=		=		=
	84		21		7		49

	√21
x =
	7

	9√21		3√7
a =		r =
	7		7

z tw. Pitagorasa

	3*3*7
4*3 =		+ b2
	7*7

	9		75		25*3*7		5√21
b2 = 12 −		=		=		→ b =
	7		7		7*7		7

	14√7
BC =		= 2√7
	7

Z tw. sinusów

	2√7		2√7		2
2R =		=		= 2√7*
	sin120		√3   2		√3

	2√21
R =
	3

Sprawdź rachunki

wredulus_pospolitus: błąd przy wyznaczaniu a i r po wyliczeniu x (na odwrót)

	√21		3√7		9√21
a = x√3 =		*√3 =		natomiast r = 9x =
	7		7		7

wredulus_pospolitus:

	√3
nie ... było dobrze ... tylko błąd był wcześniej: tgα =		−−−> a = 9x i r = √3x
	9

wredulus_pospolitus:

	9√21 + 5√21
ale |BC| = a + b =		= 2√21
	7

|BC| = √3R −−−> R = 2√7 i wychodzi jak w odpowiedzi

Saizou : Dzięki wredulus, w wersji na kartce miałem ctg α, ale potem przypomniałem sobie, że nie ma ctg w podstawie

Mila: wg rysunku Saizou 1) w ΔABC: 2α+2β+120=180 α+β=30 2) WΔBCO: α+β+|∡BOC|=180 stąd : |∡BOC|=150^o 3) |BC|²=6²+(2√3)²−2*6*2√3*cos(150^o) |BC|²=48+12√3*√3=48+36 |BC|²=84 |BC|=2√21 dalej j.w. 22:56