Dwa dowody geometryczne (trojkaty)
blug: 1. Dany jest trójkąt ostrokątny ABC o kącie przy wierzchołku C równym 60°. Punkty D i E leżą
odpowiednio na bokach BC i AC oraz <BAD = 30° i <ABE = 30°. Udowodnić, że AE = BD.
2. Odcinek CD jest wysokością trójkąta prostokątnego ABC o kącie prostym przy wierzchołku C.
Udowodnić, że AB ≥ 2CD.
20 lut 23:57
chichi:
dobrze, zacznijmy od porządnego rysunku, możesz wstawić na zapodaj.net zdjecie swojego rysunku?
21 lut 00:16
21 lut 00:35
21 lut 00:35
chichi:
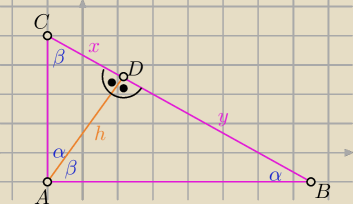mamy pokazać, że x + y ≥ 2h.
h
2 = xy ⇔ h =
√xy (z podobieństwa ΔBAD i ΔACD)
z nierówności między średnimi mamy, że: (AM ≥ GM)
| x + y | |
| ≥ √xy ⇔ x + y ≥ 2√xy = 2h □ |
| 2 | |
21 lut 01:03
chichi:
w zadaniu 1, opisując okrąg na ΔABC zauważamy iż |∡AOB| = 2|∡ACB|, gdzie O = AD ∩ BE. no, a to
z kolei oznacza, ze O jest środkiem okręgu opisanego na trójkącie ABC, co oznacza, że odcinki
AD i BE zawarte są w symetralnych boków, zatem dostajemy tam trójkąty 30,60,90 i okazuje się,
że ΔABC jest równoboczny, i z przystawani trójkątów mamy tezę
21 lut 01:50
blug: Okej dzieki wielkie.
Jeszcze pytanie, skad wiadomo, ze h2 = xy?
21 lut 15:58
Mila:
Z podobieństwa trójkątów : ΔADC∼ΔADB
21 lut 16:14
chichi:
zaznaczylem na rysunku trójkąty podobne i nawet napisałem, które
21 lut 16:14