Homograficzna Wiktoriaa: Wykrese funkcji g jest symetryczny względem prostej x=−1 do wykresu funkcji f(x)=2−x/x+3 Wyznacz wzor funkcji g.

wredulus_pospolitus:

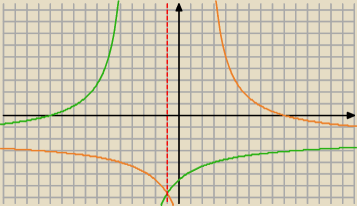
	x		2−x		x
f(x) = 2 −		czy też f(x) =		a może f(x) = 2 −		+ 3
	x+3		x+3		x

bo Twój zapis oznacza ostatnią opcję (dlatego używamy NAWIASÓW )

Wiktoriaa: Drugi zapis

wredulus_pospolitus:

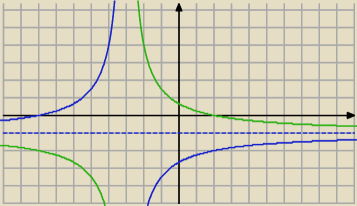
	2−x		x−2		x+3 − 5		5
f(x) =		= −		= −		= − 1 −
	x+3		x+3		x+3		x+3

1. z takiej postaci funkcji zauważyć możemy, że funkcja f(x) posiada asymptotę pionową x = −1 2. funkcja g(x) jest symetryczna względem tejże osi z funkcją f(x) ... więc także będzie posiadać tą samą asymptotę więc będziemy mieli g(x) = −1 + 'coś tam' .... i to coś tam to odbicie pozostałości funkcji f(x).

	5
czyli g(x) = −1 +
	x+3

wredulus_pospolitus: dobra ... to wszystko jest 'do dupy' przecież funkcja f(x) ma asymptotę POZIOMĄ y = −1 ... a symetria ma być względem x = −1

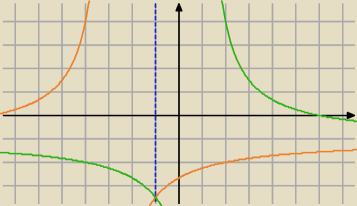wredulus_pospolitus: to wtedy tak to bym zrobił:

	5
1. f(x) = .... = −1 −
	x+3

2. tworzymy funkcję h(x) przesuwając funkcję f(x) o '1 jednostkę w prawo'

	5		5
h(x) = −1 −		= −1 −
	(x−1) + 3		x+2

3. odbijamy względem osi OY ... czyli zamiast 'x' wstawiamy '−x'

	5		5
n(x) = −1 −		= −1 +
	−x + 2		x−2

4. przesuwamy z powrotem o '1 jednostkę w lewo' otrzymując:

	5		5
g(x) = −1 +		= −1 +
	(x+1) − 2		x − 1

wredulus_pospolitus: UWAGA Dlaczego przesuwamy wykres tak, aby symetria była względem prostej x = 0 Ponieważ umiemy łatwo 'odbić' względem osi OX bądź OY czyli prostych y = 0 i x = 0 odpowiednio. UWAGA 2 Punkt 1. można pominąć, jednak lepiej sobie wyrobić ten nawyk, dodatkowo − wtedy musimy 'uważać' tylko na jednego x'a

Magdaa_00:

	10−2x
a co z wykresem gdyby było f(x)=		? jak zrobić podobne zadanie żeby powstał g(x)?
	x−2

bo coś nie idzie

wredulus_pospolitus: to pokaż jak robisz ... zobaczymy

wredulus_pospolitus: też symetria względem x = −1

wredulus_pospolitus: