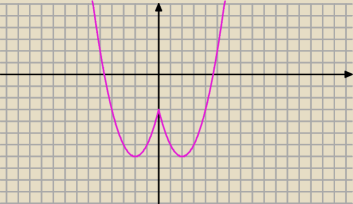
funkcja Wara: f(x)= x²−4|x|−3 f(x)= m ma trzy rozwiązania dla m?

Wara: proboje ogarnac to hamonogranem pomocniczym tylko mam jednego x zamiast dwoch albo jak sie postaram to nawet trzy (wiem ze to nie powinno sie zdarzyc w tym wypadku)

Wara: x=0 i jaki jest drugi?

chichi:

Wara: dobra to jednak o wytłumaczenie można by było prosić :,)

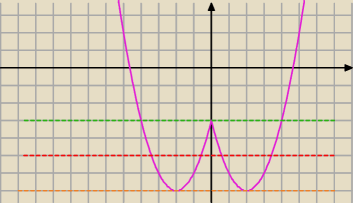
chichi: rysujemy proste równoległe do osi OX, o równaniu y = m i sprawdzamy dla jakiego 'm' będą 3 rozwiązania, z wykresu odczytujemy, że dla m = −3

wredulus_pospolitus: alternatywne podejście (mniej sztampowe, bardziej "szprytne"): 1. zauważamy, że funkcja f(x) jest funkcją parzystą: f(−x) = (−x)² − 4|−x| − 3 = x² − 4|x| − 3 = f(x) związku z tym, jeżeli równanie f(x) = m ma rozwiązanie dla jakiegoś x_a > 0 ... to także ma rozwiązanie dla takiego x_b<0 , że x_a + x_b = 0 co za tym idzie −−− równanie f(x) = m może mieć DOKŁADNIE 3 rozwiązania (a konkretniej − nieparzystą liczbę rozwiązań) wtedy i tylko wtedy, gdy jednym z tych rozwiązań będzie x=0 f(0) = 0 − 4*0 − 3 = −3 −−−> czyli jedyną możliwą (ale nadal nie wiemy, czy prawidłową) wartością dla parametru m jest m = −3 wystarczy teraz sprawdzić czy będziemy mieli dokładnie 3 rozwiązania (jedno już znamy) dla równania f(x) = −3 x² − 4|x| −3 = −3 x² − 4|x| = 0 (|x|)² − 4|x| = 0 |x|*(|x| − 4) = 0 −−−> rozwiązania: x = 0 lub x = −4 lub x = 4 Odp: Dla m = −3 równanie f(x) = m ma dokładnie trzy rozwiązania

wredulus_pospolitus: a 'szprytne' −−− bo na teście od razu byśmy mogli zawęzić pole poszukiwań. A na teście 'czas to pieniądz'