planimetria
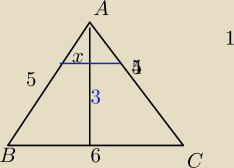
Magdaa_00: Trójkąt ABC, w którym AB=AC=5m oraz BC=6m, jest częściowo wypełniony wodą. Gdy
trójkąt leży na boku BC, poziom powierzchni wody znajduje się 3m ponad bokiem. Na jakiej
wysokości w metrach znajduje się powierzchnia wody, gdy trójkąt leży na boku AB?
20 lut 09:01
.:
Do rozwiązania tego zadania będzie konieczna znajomość :
1. Tw. Pitagorasa (w celu wyznaczenia wysokości trójkąta gdy BC jest podstawą)
2. wzor na pole trójkąta (do policzenia pola a później wyznaczenie a drugiej wysokości)
3. wniosek z Tw. Talesa (do wyznaczenia górnych podstaw trapezow/długości lustra wody)
4. wzór na pole trapezu
20 lut 09:18
Wiktoriaa: Mi wyszło 2m,czy jest ok?
20 lut 10:46
kerajs:
Przypuszczam, iż autor tego absurdalnego ''zadania'' oczekiwał się odpowiedzi 18/5
20 lut 11:17
Jolanta:
h
2+3
2=5
2
h
2=25−9
h
2=16
h=4
maly trojkat jest podobny do duzego ,wysokosc tego trojkata 4−3=1
4x=3
x=
34
gorna podstawa trapezu 2*{3}{4}=1
12
| | 12 | |
Wysokosc opuszczona na bok AC h= |
| =2 25 |
| | 5 | |
| | 18 | |
odpowiedz |
| to jakby za duzo |
| | 5 | |
20 lut 11:40
wredulus_pospolitus:
@Jolanto −−− jakim cudem wysokość opuszczona na AC jest mniejsza od tej opuszczonej na AB
przecież |AC| < |AB|
Zapomniałaś przemnożyć przez 2
20 lut 12:40
wredulus_pospolitus:
Może zaprezentuję też alternatywne podejście do tego które wcześniej przedstawiłem:
0. Obliczamy z pitagorasa h
AB = 4
1. skala wysokości: Trójkąt 'powietrza' gdy podstawą jest AB do trójkąta ABC wynosi:
(ewentualnie można dorzucić)
więc skala PÓL tych trójkątów to (0.25)
2
2.
Po przewróceniu na inną podstawę, pole trójkąta pozostało takie samo ... także pole 'powietrza'
będzie takie same co wcześniej.
Związku z tym ... skala PÓL nadal wynosi (0.25)
2.
| | 1 | |
Związku z tym skala wysokości nadal będzie wynosić : |
| |
| | 4 | |
3.
| | 3 | |
Więc wysokość słupa wody to nadal będzie |
| htrójkąta ABC |
| | 4 | |
| | 18 | |
4. wyznaczamy hAC = 4.8 −−−> xszukana wysokość = 3.6 = |
| |
| | 5 | |
20 lut 13:02
Jolanta: Oczywiście 🙂chciałam szbko policzyc a warunki nie pozwalaja
20 lut 13:05
Jolanta: Sytuacja ogarnieta to moge na spokojnie dokonczyc
Chciałam zrobić tak
P
Δ−P
t=P
mΔ
12−11
14=
34
trojkaty sa podone skala podobienstwa =k
2
k
2=16
k=4
duzy trójkat ma 4 razy wieksza wysokosc niz maly(h
mΔ=1/4 h)
h
t=3/4 h
20 lut 13:45
Mila:
Litości−"trójkąt wypełniony wodą" ?
20 lut 14:26
Jolanta: Proponuję zadanie Jaka objętość musi mieć cząsteczka wody,żeby uznać ją za figurę płaska 🤔
20 lut 18:19
Saizou : Żadna, figury płaskie mają dwa wymiary.
20 lut 18:23
Jolanta: Wiem🤣 Dlatego takie zadanie to dezinformacja dla ucznia
20 lut 18:51