Nierówność i stosunek boków trójkąta Nebula : Witam, mam problem z dwoma zadankami, co do jednego nie jestem pewny odpowiedzi a w drugim nie wiem co mam dalej zrobić. Zad. 1 Rozwiąż nierówność

	2x+7		2x+72
1−		+		− ... ≥ 2.
	2		4

Rozwiązanie zapisz w postaci przedziału liczbowego. Obliczyłem, że moje q = {−2x+7}{2}

	−2x+7
Wykorzystałem wzór na nieskończoną sumę ciągu lim(n→∞) Sn = |		| < 1 , czyli dalej mi
	2

wyszło, że

−2x+7		−2x+7
	< 1 ⋁		> −1
2		2

	5		9
I wyszło mi że x∊(		;		)
	2		2

	1
Na koniec podstawiłem sumę do tej nierówności		≥ 2
	1+2x+7

−4x−16
	≥ 0
2x+9

	9
i wyszło mi że x∊<−4;		>
	2

	5		9
porównując oba przedziały wyszło mi że końcowy przedział wynosi x∊(		;		)
	2		2

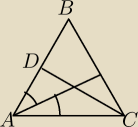
czy jest to poprawna odpowiedź? Zad.2 Środkowa CD trójkąta ABC jest prostopadła do dwusiecznej AE tego trójkąta. Oblicz stosunek

	AE
	AB

Tu na podstawie rysunku zauważyłem tylko że są one chyba podobne do siebie na podstawie cechy BKB. Z góry dziękuje za odpowiedzi

ite: Czy nierówność wygląda tak?

	2x+7		(2x+7)2
1−		+		− ... ≥ 2
	2		4

	−(2x+7)
Wtedy q =
	2

.: 1) mianownik: 1 + 2x + 7 = 2x + ile A ile ty masz? Licznik także błędnie.

	1
A druga sprawa... Zauważ że:		≥ 2 − − − − > 0 < a ≤ 0.5
	a

Z takiej podwójnej nierówności odrobinkę szybciej będzie, nie sądzisz?

Nebula:

	−5
Czyli w takim razie końcowy przedział w pierwszym zadaniu wynosi x∊< −4 ;		)
	2

Tak?

.: A niby dlaczego

Nebula : Poprawiłem faktycznie błędnie zapisane przeze mnie q i wykonałem ponownie obliczenia i taki mi wynik wyszedł jeśli to nie jest poprawny wynik to już nie wiem gdzie mam błąd

Jolanta: Dla q wyszedł mi przedział <−4,5;−2,5> A dla S ≥2. Przedział (−4,5;−4] Część wspólna (−4,5;−4]

wredulus_pospolitus: po pierwsze:

	2x+7		2x+7
q = −		; |q| < 1 ⇒ |		| < 1 ⇔ −2 < 2x+7 < 2 ⇔ −9 < 2x < −5 ⇔
	2		2

x ∊ (−4.5 ; −2.5) po drugie:

	1		2
S =		=
	2x+7   1 +   2		2x+9

	1
S ≥ 2 ⇔		≥ 1 ⇔ 0 < 2x+9 ≤ 1 ⇔ x ∊ ( −4.5 ; −4 ]
	2x+9

Nebula : Faktycznie zauważyłem gdzie zrobiłem błąd i wyszedł mi ten sam wynik.

	AC
W zadaniu 2 zauważyłem że ten stosunek		wynosi 1/2
	AB

SzymonZc: Dobrze, że Nebula naprawiła błąd w obliczeniach i teraz masz ten sam wynik. Tutaj są dobre gry do rozwijania logiki https://boskatv.pl/