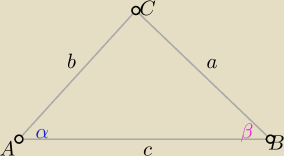
| c2 | ||
PABC= | ||
| 2(ctgα+ctgβ) |
| a | c | c sinα | ||||
albo: z twierdzenia sinusów: | = | ⇒ a = | ||||
| sinα | sin(α+β) | sin(α+β) |
| 1 | 1 | c sinα | ||||
Pole trójkąta P = | ac sinβ = | * | *c*sinβ = | |||
| 2 | 2 | sin(α+β) |
| c2 sinα sinβ | ||
= | i jeszcze można inaczej | |
| 2sin(α+β) |
Holmes 
wywołał mnie ......... 
to
| c | ||
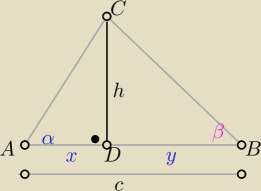
x= h*ctgα , y= h*ctgβ to x+y=c = h(ctgα+ctgβ) ⇒ h= | ||
| ctgα+ctgβ |
| 1 | ||
PABC= | *c*h | |
| 2 |
| c2 | ||
PABC= | ||
| 2(ctgα+ctgβ) |