proszę o rozwiązanie anna: dany jest prostokąt ABCD o bokach BA= 2 oraz BC =1 Na bokach BC oraz CD obrano odpowiednio Punkty E i F takie że : CE = x oraz CF =1/x Oblicz dla jakiej wartości x pole trójkąta AEF jest najmniejsze

.:

	1
Zauważ że PΔ = 0.5*|CE|*|CF| =0.5 * x *		= 0.5
	x

Pole będzie miało stała wartość. Jedyne co musisz jeszcze zrobić to POPRAWNIE wskazać w jakim przedzie tak naprawdę możemy wybrać x

.: Nie przedzie tak tylko miało być w przedziale

anna: czy te trójkąty są prostokątne skoro tak obliczone pole

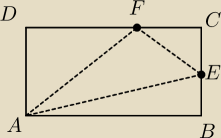
wredulus_pospolitus: Byłem zaspany i nie przeczytałem o który trójkąt chodzi jednak wnioski z tamtego będą potrzebne (pole jest stałe ... musisz dobry przedział 'x' wyznaczyć)

	1		x		1
PAEF = 2 − PADF − PABE − PCEF = 2 −		−		−		=
	2x		2		2

	3−x		1
=		−
	2		2x

pochodna i szukasz minimum

anna: pole trójkąta ADF =( 2−¹_x)/2 = P₁ = 1 − ¹_2x pole trójkąta ABE = 2*(1 − x)/2 = x−1 = P₂ pole trójkąta CFE = x*¹_x/2 = ¹₂ = P₃ P₁ + P₂ +P₃ = 1 − ¹_2x + x−1 + ¹₂ pole trójkąta AEF = 2 − ( 1 − ¹_2x + x−1 + ¹₂) = 2 + ¹_2x − x − ¹₂ pole trójkąta AEF = ^{3 −x}₂ + ¹₂ = P(x) ale wynik w odpowiedzi jest że pochodna ma wzór P^,(x) = ^{2x2 −1}_2x² co jest niepoprawne

anna: przepraszam za pomyłkę pole trójkąta AEF = ^3−x₂ + ¹_2x

anna: dziękuję