proszę o rozwiązanie

proszę o rozwiązanie anna: dany jest trójkąt ABC w którym punkty D i E leżą odpowiednio na bokach AB i AC tak że zachodzą warunki I AD I : I DB I = 1 :2 oraz I AE I : I EC I = 3 : 1 Odcinki BE i CD przecięły się w punkcie O Prosta AO przecina bok BC w punkcie F oblicz stosunek BF do CF

13 lut 20:49

Eta:

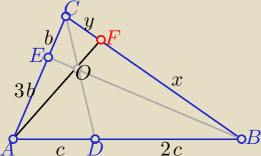
Z tw. Cevy

\|AD\|		\|BF\|		\|CE\|
	*		*		=1
\|DB\|		\|FC\|		\|EA\|

1		x		1
	*		*		=1 /*6y
2		y		3

x= 6y

	\|BF\|
to		=6:1
	\|FC\|

13 lut 21:52

anna: dziękuję ale w zadaniu była uwaga aby nie korzystać z tw Cevy

13 lut 22:07

Saizou : To skorzystaj z dowodu tego twierdzenia (tylko zamiast rozważań na literkach masz liczby)

13 lut 22:13

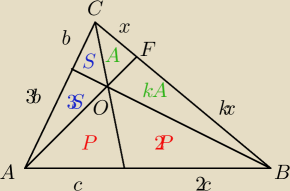
Saizou : rysunek

	BF		kx		k
Szukamy		=		=
	FC		x		1

	P		4S+P
(1)		=		−−>(1+k)A=8S
	2P		(1+k)A+2P

	S		S+(1+k)A
(2)		=		−−> (1+k)A = P
	3S		3S+3P

Z (1) i (2) mamy, że P=8S

A		A+4S
	=		→ 3P = 4kS
kA		kA+3P

3*8S =4kS k = 6 BF : DC = 1:6

13 lut 23:51

Saizou : Oczywiście BF : DC = 6:1

13 lut 23:54

Saizou : Późno jest... BF : FC = 6:1

14 lut 00:11

anna: dziękuję bardzo

14 lut 16:02

\|AD\|		\|BF\|		\|CE\|
	*		*		=1
\|DB\|		\|FC\|		\|EA\|