równanie z parametrem silco: wyznacz te wartości parametru m (m∊R) dla których równanie |16−x²|= (m+4)² −9 ma dwa różne rozwiązania

.: Niech f(x) = 16 − x² Rozwiazujesz: 0 = (m+4)² − 9 ∨ f(x_wierzchołka) < (m+4)² − 9

silco: hmm, tylko dlaczego akurat tak generalnie zacząłem to rozwiązywać trochę inaczej i w sumie doszedłem tylko, że dla m=−7 lub m=−1, czyli to samo co by wyszło z pierwszego przypadku, który podałeś

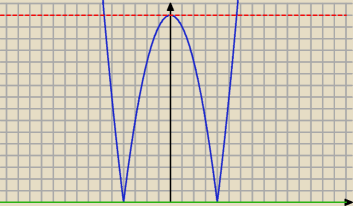
wredulus_pospolitus: w tego typu równaniu warto sobie z boku zrobić szkic wykresu. zielona linia reprezentuje rozwiązanie f(x) = 0 albo jak wolisz |16−x²| = 0 natomiast czerwona linia reprezentuje prostą y = f(x_wierzchołka) = y_wierzchołka zauważ, że każda prosta 'powyżej' y_wierzchołka będzie dwukrotnie przecinać niebieski wykres. Stąd ten drugi warunek

silco: n ok, powiedzmy, że rozumiem ale jakbym chciał bez robienia rysunków pomocniczych? jak to "zauważyć"?

wredulus_pospolitus: jeżeli nie kojarzysz nawet wykresu ... to może być ciężkawo ... jedyne co pozostaje to rozwiązać równanie: |16−x²| = k i zobaczyć dla jakich 'k' będą tylko dwa rozwiązania (a później zrobić k = (m+4)² − 9)

wredulus_pospolitus: w momencie gdy jest to zadanie na maturze ... jest to po prostu strata czasu

wredulus_pospolitus: no ale na szybkiego przedstawię szkic: na początek zauważamy, że dla k<0 mamy 0 rozwiązań (bo lewa strona równania przyjmuje wartości nieujemne ) 1. x ∊ [−4; 4] , k ≥ 0 16 − x² = k −−−> 16 − k − x² = 0 −−−> (√16−k − x)(√16−k + x) = 0 −−−> czyli dla k = 16 mamy jedno rozwiązanie , dla k ∊ [0; 16) mamy dwa rozwiązania UWAGA. drugi przedział uwzględnia warunek dla tego przypadku (1) 2. x ∉ [−4; 4] , k ≥ 0 x² − 16 = k −−−> x² − (16+k) = 0 −−−> (x− √16+k)(x + √16+k) = 0 −−−> czyli dla rozwiązania będą dla każdego k > 0 (uwzględnia warunek (2) ) W efekcie mamy: a. 2 rozwiązania dla k = 0 i k > 16 b. 3 rozwiązania dla k = 16 c. 4 rozwiązania dla k ∊ (0; 16) d. 0 rozwiązań dla k < 0