stereometria JacekJacek: Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości b i kącie przy wierzchołku równym α. Przekątne dwóch ścian bocznych tworzą z podstawą kąt β. Oblicz objętość tego graniastosłupa. Powinno wyjść ( 0,5b³ sinα tgβ)

.: Rysunek i czy jesteś w stanie zaznaczyć kat β Czy wiesz co to za kat?

.: Bo: 0.5b²sinα powinno być dla Ciebie logiczne, że jest to pole podstawy. Więc pozostaje jedynie wyznaczenie wysokości tego graniastoslupa

JacekJacek: No właśnie kąt β jestem w stanie zaznaczyć, natomiast nie rozumiem skąd się bierze to pole podstawy, dlaczego to jest 0,5b²sinα

.: Wracamy do zadań z pola trójkąta. Jednym ze wzorów na piłę trójkąta jest: 0.5*a*b*sinα Gdzie a,b długości sąsiadujących boków natomiast α to KAT POMIEDZY TYMI BOKAMI. Tutaj w zadaniu masz trójkąta równoramienny i kat między ramionami wynosi α Stąd pole podstawy to 0.5*b*b*sinα czyli 0.5b²sinα

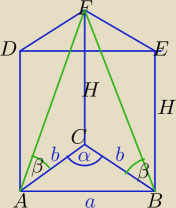
Mila: W ΔACE:

	h
tgβ=
	b

H=b*tgβ

	1
V=		b2 sinα*b*tgβ
	2

	1
V=		b3sinα*tgβ
	2

============

.: A jeszcze wracając do tego wzoru na pole trójkąta. Wynika on że 'standardowego wzoru na pole' i informacji czym jest sinus kąta. Zrób sobie rysunek. Narysuj sobie trójkąta. Niech podstawa będzie bokiem a. Kat pomiędzy a i b będzie równy α. Zaznacz wysokość tego trójkąta opadająca na bok a. Czemu jest równy sinα W takim razie czemu jest równy b*sinα Podstawiasz i masz wzór na pole.

JacekJacek: juz rozumiem, dziękuję