Zadanie z kwadratem dla chętnych licealistów.
Mila:
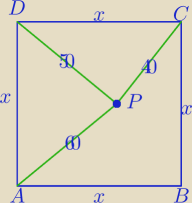
ABCD− kwadrat
|PA|=60
|PC|=40
|PD|=50
Oblicz dł. boku kwadratu.
4 lut 22:23
chichi:
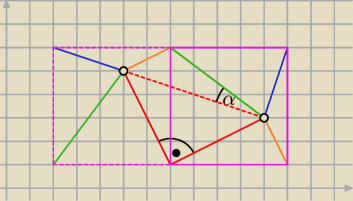
zostawię rysunek do sprytnego rozwiązania

4 lut 23:04
Mila:

4 lut 23:25
Kacper: 
5 lut 17:20
an: Licealiści niezbyt chętni , mnie z analitycznej i równań 3 okręgów wyszło
| | 52+√2300 | |
x=10√ |
| ≈70,69593879 |
| | 2 | |
i jest to raczej prawidłowy wynik, czy Milu potwierdzasz
6 lut 13:35
getin:
Ja robiłem trochę inaczej bo ułożyłem układ 3 równań
a2+b2=502
(x−a)2+b2=602
a2+(x−b)2=402
i mi z niego wyszło tyle samo bo x = 10√26+5√23
6 lut 14:42
Mila:
an, getin, potwierdzam wynik

6 lut 15:46
.:
Połowa z nich na feriach, reszta się szykuje do ferii, a Wy im dajecie zadania do rozwiązywania
6 lut 16:25
Mila:
Przeskalowałam wymiary − łatwiejsze rachunki.
1) Rozwiązanie z obrotem.
2)
Rozwiązanie z układem równań.
Wychodzi równanie dwukwadratowe , jedno z rozwiązań dodatnich odrzucone.
x<40+50 i x>10
W rozwiązaniu z obrotem nie ma tego problemu.
6 lut 17:18
Mila:
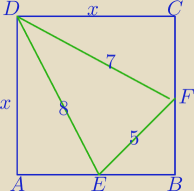
Zadanie z Olimpiady.
ABCD − Kwadrat
|EF|=5, |DE|=8, |DE|=7
Oblicz dł. boku kwadratu.
odp.
6 lut 17:28
Saizou :
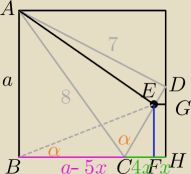
Pewnie jest prostszy sposób.
α = 60°
AE = 4
√3
Na czworokącie ABCE można opisać okrąg.
<EBC = 60° (oparty na łuku AE)
CE = 4 oraz ED = 1
ΔCFE ~ ΔCHD ~ ΔCHD
| | √3 | | 2√3 | |
ΔBFE jest trójkątem 30, 60, 90, zatem BF = a−x, FE = |
| (a−x), BE = |
| (a−x) |
| | 3 | | 3 | |
Z tw. Ptolemeusza dla ABCE mamy
| | 2√3 | |
8• |
| (a−x) = 4√3•(a−5x) + 4a |
| | 3 | |
...
Z tw. Pitagorasa w ABC
...
12 lut 14:18
Saizou : Eta znasz prostszy sposób?
13 lut 21:59
Saizou : Mila może ty masz inny sposób?
14 lut 20:34
Mila:
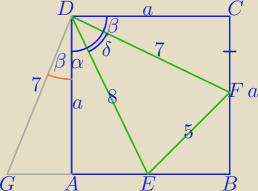
Mam inny sposób. Nie wiem czy wyda się Wam prostszy.
α+β=90−δ,
Dorysowany Δ GAD.
1) w ΔDEF:
25=64+49−2*8*7cosδ
sin(α+β)=sin(90−δ)=cosδ
| | 5√3 | |
cos(α+β)=sinδ, sinδ= |
| |
| | 14 | |
2)
W ΔGED:
|GE|*a=44
|GE|
2=49+64−2*7*8 cos(α+β)
| | 5√3 | |
|GE|2=113−2*7*8* |
| =113−40√3 |
| | 14 | |
3)
================
14 lut 21:16
Saizou : Ciekawy pomysł z tym dorysowaniem trójkąta.
Z jakiej olimpiady to zadanie?
Zawsze mnie zastawilo skąd biorą się takie zadania. W sensie, w jaki sposób są one tworzone.
14 lut 21:23
Saizou : Do tego jeszcze nie usiadłem, będę się głowić w najbliższym czasie.
Dziękuję Mila.
Jestem ciekaw czy Eta coś dorzuci od siebie.
14 lut 22:18
Mila:
Czekamy na
Etę.

14 lut 22:49
Eta:
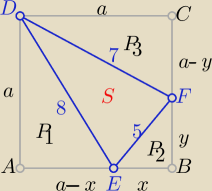
Może tak :
S −− z Herona
a
2= P
1+P
2+P
3+S
i Pitagoras
w AED i EBF i FCD
nie liczyłam

bo boli mnie głowa od paru dni .. ..
Myślę,że sposób podany przez
Milę jest najprostszy
Pozdrawiam

15 lut 23:06
Eta:
a2 miało być
15 lut 23:09
Saizou : Dzięki Eta, ale jak zaprzęgać Pitagorasa w takiej postaci, to sam on wystarczy. Jutro
przeliczę.
Teraz kminię to pierwsze.
Dużo zdrówka dla Ciebie.
15 lut 23:14
Mila:
Zdrowia
Eta,
Ostatnio są wahania pogodowe. Mnie też dzisiaj głowa bolała, co bardzo rzadko się zdarza.
Przeszło po kawie.
Pozdrawiam

16 lut 01:19
Min. Edukacji: Przypominam, że na ferie się nie zadaje😄
16 lut 04:15
Kacper: 
16 lut 20:42
 ABCD− kwadrat
|PA|=60
|PC|=40
|PD|=50
Oblicz dł. boku kwadratu.
ABCD− kwadrat
|PA|=60
|PC|=40
|PD|=50
Oblicz dł. boku kwadratu.
 zostawię rysunek do sprytnego rozwiązania
zostawię rysunek do sprytnego rozwiązania 



 Zadanie z Olimpiady.
ABCD − Kwadrat
|EF|=5, |DE|=8, |DE|=7
Oblicz dł. boku kwadratu.
odp.
Zadanie z Olimpiady.
ABCD − Kwadrat
|EF|=5, |DE|=8, |DE|=7
Oblicz dł. boku kwadratu.
odp.
 Pewnie jest prostszy sposób.
α = 60°
AE = 4√3
Na czworokącie ABCE można opisać okrąg.
<EBC = 60° (oparty na łuku AE)
CE = 4 oraz ED = 1
ΔCFE ~ ΔCHD ~ ΔCHD
Pewnie jest prostszy sposób.
α = 60°
AE = 4√3
Na czworokącie ABCE można opisać okrąg.
<EBC = 60° (oparty na łuku AE)
CE = 4 oraz ED = 1
ΔCFE ~ ΔCHD ~ ΔCHD
 Mam inny sposób. Nie wiem czy wyda się Wam prostszy.
α+β=90−δ,
Dorysowany Δ GAD.
1) w ΔDEF:
25=64+49−2*8*7cosδ
Mam inny sposób. Nie wiem czy wyda się Wam prostszy.
α+β=90−δ,
Dorysowany Δ GAD.
1) w ΔDEF:
25=64+49−2*8*7cosδ

 Może tak :
S −− z Herona
a2= P1+P2+P3+S
i Pitagoras
w AED i EBF i FCD
nie liczyłam
Może tak :
S −− z Herona
a2= P1+P2+P3+S
i Pitagoras
w AED i EBF i FCD
nie liczyłam  bo boli mnie głowa od paru dni .. ..
Myślę,że sposób podany przez Milę jest najprostszy
Pozdrawiam
bo boli mnie głowa od paru dni .. ..
Myślę,że sposób podany przez Milę jest najprostszy
Pozdrawiam 

