oblicz pole powierzchni ściany ABH
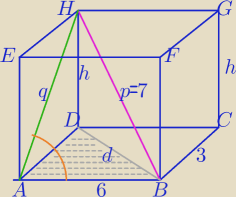
markon: W prostopadłościanie ABCDEFG dane są IABI=6 IBCI=3 oraz IBHI=7 gdzie AB i BC są krawędziami
podstawy, a BH jest przekątną tego prostopadłościanu.
Oblicz pole powierzchni ściany ABH w ostrosłupie ABDH o podstawie trójkątnej ABD i krawędziach
bocznych
AH,BH,DH, zawartego w tym prostopadłościanie. Zapisz obliczenia.
https://imgur.com/pZ68SLB rysunek w linku.
Prosiłbym o pomoc.
1 lut 16:04
wredulus_pospolitus:
A z obliczeniem której ściany masz problem
Czy potrafiłeś wyznaczyć wysokość tego prostopadłościany (i zarazem ostrosłupa)
1 lut 16:11
wredulus_pospolitus:
tak naprawdę musisz policzyć:
1. wysokość prostopadłościanu / ostrosłupa
2. przekątną ściany bocznej ADHE
ściana ABH jest trójkątem prostokątnym o przyprostokątnych AB (masz długość) i AH ( czyli
przekątna ADHE)
1 lut 16:13
markon: Nie wiem jak obliczyć odcinek I DB I. Jak już to będę miał to dalej wiem co robić.
1 lut 16:35
wredulus_pospolitus:
Przecież BD to przekątna podstawy
AB masz, a przecież AD = BC
1 lut 16:43
Mila:
1) d
2=9+36, d
2=45
d=3
√5
2)
w ΔDBH:
7
2=45+h
2, h
2=4, h=2
3) w ΔADH:
q
2=2
2+3
2, q=
√13
4)
Pł. ABCD⊥pł. ADHE,
AB⊥pł. ADHE⇒z T
3⊥, że AB⊥AH
5)
sprawdź rachunki
1 lut 16:52
markon: Dzięki za pomoc.
1 lut 17:03