Optymalizacja rozszerzenie
djnajak: Dana jest funkcja f(x)=4x/(x
2+1) określona dla x należącego do przedziału [−5; 5].
Rozpatrujemy wszystkie trójkąty ABC, których wierzchotki A i B są punktami wspólnymi wykresu
funkcji f oraz prostej y = m, gdzie m>=1,
natomiast C = (0, −2).
Oblicz współrzędne wierzchołków A i B, dla których pole trójkąta ABC jest największe.
| | 2√4−m2 | |
Mam podstawę AB, ktora lezy na prostej y=m, ktora wynosi |
| oraz wierzchołek C |
| | m | |
(0,−2).
Jak obliczyć wysokość h, która ma wyniesc m+2?
probowałem z ze wzorem na odleglosc punktu od prostej ale nie wychodzi, proszę o pomoc.
 https://brainly.pl/zadanie/22171896
https://brainly.pl/zadanie/22171896
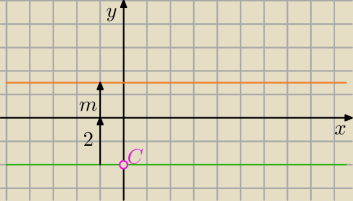
 C = (0,−2), y − m = 0 zatem
C = (0,−2), y − m = 0 zatem