ostrosłup adrian: Oblicz objętość czworościanu ABCD, jeżeli AB = 2, AC = AD = BC = BD = 3, CD = 5

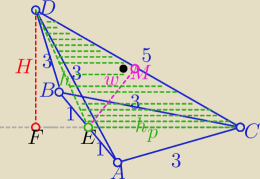
Eta: ΔDEC jest przekrojem ostrosłupa i jest trójkątem równoramiennym zatem H = |DF| −−− zewnętrzna wysokość ΔDEC i jest wysokością ostrosłupa teraz tylko obliczenia: |EC|=|DE|=2√2

	√7
|EM|=w= √8−(5/2)2 =
	2

	1		√7		5√7
P(DEC)=		*5*		=
	2		2		4

	1
i P(DEC)=		H*|EC| ⇒P(DEC)=√2H
	2

	5√7
to H=
	√2

	1
Pp=P(ABC)=		*2*2√2 = 2√2
	2

	1
V=		Pp*H
	3

	5√7
V=
	6

===========