Wyznacz objetość ostrosłupa
wojtek: Wyznacz objetość ostrosłupa prawidłowego czworokątnego, ktorego pole powierzchni bocznej jest
równe P, a kąt między wysokościami ścian bocznych opuszczonymi z wierzchołka ostrosłupa ma
miarę 2α. Rozważ dwa przypadki.
Prawidłowe odpowiedzi to: P/6*cosα*
√P*sinα i 2
1/4/6*P*
√P*sinα*(1−2*sin2α)
Jedyne co udało mi się zrobić to wyznaczyć długości krawędzi podstaw:
√P*sinα i
2
1/4*
√P*sinα
Ale prawdopodobnie są one nieprawidłowe albo robię jakiś błąd, bo dalej nic nie wychodzi
Eta:
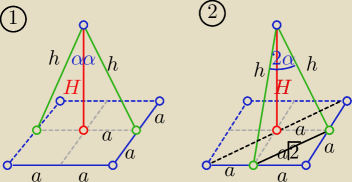
W 1) 2a=
√Psinα ( masz dobrze)
P
p= 4a
2= Psinα
| | √Psinα*cosα | |
i H= actgα ⇒ H= |
| |
| | 2sinα | |
V=.......
==================
2) 2a=
4√2√Psinα −−− też masz dobrze
z tw. cosinusów
(a
√2)
2=h
2+h
2−2h
2cos2α
2a
2= 2h
2(1−cos2α) ⇒...........
Z tw. Pitagorasa
H
2=h
2−a
2
H=..........
P
p= 4a
2=.....
V= ..... otrzymasz wynik jaki masz w odpowiedzi