Czy mogę prosić o sprawdzenie, czy mam dobrze to zadanie z wart. bezwzględną? Monika: Dzień dobry. Czy mogę prosić o sprawdzenie, czy mam dobrze to zadanie z wart. bezwzględną? U Was zawsze dostaję wsparcie. dziękuję za poświęcony czas: https://zapodaj.net/plik-wIvZOQyD0n

ABC: od razu w linijce pod zielonym I rzymska , dlaczego opuściłeś wartość bezwzględną? to że x≥0 wcale ci nie gwarantuje że mx≥0 , bo może być m<0

Monika: Aha, słusznie. Cenna uwaga. Czyli już tu muszę wziąć pod uwagę także m<0 lub m ≥0 tak?

MiKa: |m*x|= |m|*|x|

Monika: ABC, wzięłam pod uwagę Twoją podpowiedź. MiKa, już nie chciałam zmieniać toku myślenia, ale dziękuję za wskazówkę. Wyszły mi w dyskusji 2 rozwiązania, albo sprzeczne. Proszę Was o spojrzenie, czy teraz już mam dobrze? https://zapodaj.net/plik-LjOT9AYHeL

ABC: wygląda dobrze na pierwszy rzut oka

wredulus_pospolitus: odnośnie warunku: x ≥ 0 i m < 0 i m ≠ 1

	m
zauważ, że rozwiązanie: x =		nie ma rozwiązań
	−m+1

	liczba ujemna
zauważ, że po prawej stronie równania mamy
	liczba dodatnia

związku z tym jak liczba nieujemna (x) ma być równa liczbie ujemnej (ułamek)

ABC: no mówiłem na pierwszy rzut oka

wredulus_pospolitus: odnośnie warunku: z x < 0 <−−−− przyjrzyj się im ... bo nie zawsze są one spełnione

wredulus_pospolitus: alternatywny sposób podejścia do sprawy: |mx| + x = m |m|*|x| + x = m 1. x ≥ 0 |m|*x + x = m x*(|m| + 1) = m

	m
x =		<−−− zauważamy, że bez względu na wartość 'm' w liczniku będzie wartość
	1+ |m|

dodatnia, związku z tym: dla m ≥ 0 mamy 1 rozwiązanie, dla m < 0 brak rozwiązań 2. x < 0 −|m|*x + x = m x(1−|m|) = m // zał. m ≠ ± 1 //

	m
x =		<−−− zauważamy, że mianownik nie zawsze będzie dodatni − trza rozpatrzeć
	1−|m|

dodatkowe przypadki .....

Monika: Od tak długiego czasu siedzę nad tym zad. że już mam kwadratową głowę. Chyba sobie odpuszczę, brak mi siły. Bardzo Wam wszystkim dziękuję.

wredulus_pospolitus:

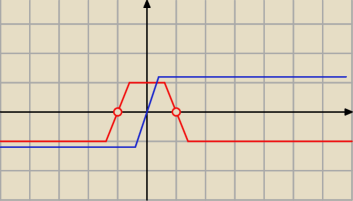
	m
można też problem		rozwiązać graficznie:
	1− |m|

gdzie czerwony oznacza znak mianownika (dodatni czy ujemny), natomiast niebieski to znak licznika. wiemy że '−' = '+' * '−' związku z tym będziemy mieli przedziały (−1 ; 0) oraz (1, + ∞) <−−− dla takich 'm' istnieje rozwiązanie takie rozwiązanie, że x < 0 W efekcie mamy: równanie ma:

⎧	0 rozwiązań dla m ≤ −1
⎨	1 rozwiązanie dla m ∊ (−1 ; 1 >
⎩	2 rozwiązania dla m > 1