Dany jest trójkąt ABC ttd: Dany jest trójkąt ABC o długościach |AB|=a, |BC|=b, |AC|=c takich, że a>b>c. Największy kąt trójkąta ABC jest 2 razy większy od najmniejszego z kątów w tym trójkącie.Wykaż, że. a)trójkąt ABC jest ostrokątny b)długości boków trójkąta ABC spełniają równość a²=c(b+c)

ABC: pójdzie z tw sinusów choć są krótsze sposoby, chytre dorysowanie Ety na przykład

Eta:

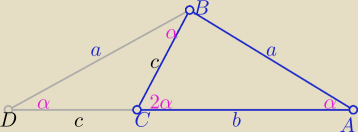
Eta: Z podobieństwa trójkątów równoramiennych ABC i ADC z cechy (kkk)

	a		c
mamy		=		⇒ a2=c(b+c)
	c+b		a

i po ptokach

Eta: a) a>b>c i 2α −− miara największego kąta trzeba wykazać,że cos2α>0 z tw. cosinusów

	b2+c2−a2
cos2α=		i a2= c2+bc z poprzedniego
	2bc

	b−c
cos2α=		>0 bo b>c
	2c

ΔABC jest ostrokątny

ttd: Dziękuje, próbowałem robić z sinusów ale raczej nie o to chodziło.

ABC: z tw sinusów sprowadzi się do wykazania tożsamości trygonometrycznej , trochę wprawy i też idzie

Mila: b) Można z tw. o dwusiecznej.

Saizou : Z tw. sinusów mamy cosα =.... (trzeba znać zależność sin(2α) =2sinαcosα) Z tw. cosinusów wychodzi zależność... trzeba znać wzór a²−b²