Równoległobok - kąt i pole jbs: W równoległoboku ABCD, |AB| > |BC|, kąt przy wierzchołku D jest rozwarty. Z punktu D poprowadzono wysokości DE i DF, gdzie E ∊ AB, F ∊ BC. Wiedząc, że |DE| = 6, |DF| = 9 oraz sinus kąta EDF jest równy 0,75, oblicz: a) Pole równoległoboku ABCD b) Pole czworokąta EBFD

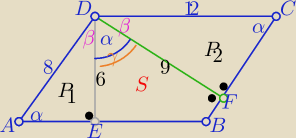
Eta: α+β=90^o α+2β+γ=180^o ⇒ γ=α

	6		3		9		3
sinα=3/4 to		=		⇒ b=8 i		=		⇒ a=12
	b		4		a		4

a) P(ABCD)= 72 b) S= P−(P₁+P₂) z tw. Pitagorasa |AE|= √7/4 i |CF|= 3√7 P₁= .... i P₂=...... dokończ........