proszę o o rozwiązanie anna: na prostej o równaniu y = 3x − 3 znajdź wszystkie punkty których odległość od punktu A(0 ,3) jest równa 3√2

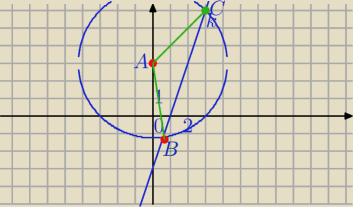
Mila: k: y = 3x − 3 o: x²+(y−3)²=(3√2)² B, C − punkty przecięcięcia okręgu i prostej k

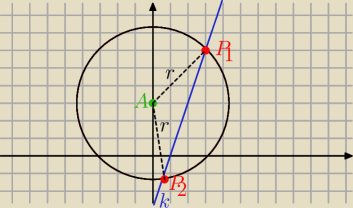
Eta: r=3√2 =|PA| r²=|PA|²= 18 P=(x, 3x−3) A=(0,3) dokończ..

Jolanta: Mamy do rozwiazania układ równań prosta i okrag y=3x−3 x²+(y−3)²=(3✓2)² x²+(3x−3−3)²=9*2 x²+9x²−36x+36−18=0 10x²−36x+18=0 /:2 5x²−18x+9=0 Δ=(−18)²−4*5*9=144

	18−12		3
x1=		=		. x2=..=3
	2*5		5

	3		1
y1=3*		−3=−1		. y2=...6
	5		5

P₁(3/5;−11/5). P₂(3;6)

anna: dziękuję