geometria analityczna basia: . Wyznacz współrzędne wierzchołków B i D czworokąta ABCD, jeśli wiadomo, że: jest on kwadratem oraz A(−3, 5) i C(5, 1). Mam to rozwiązać nie za pomocą wektorów

Jolanta: Zaznacz A i C w układzie współrzędnych |AC| to długość przekątnej kwadratu leży na prostej ,której współczynnik kierunkowy a możemy obliczyć korzystając ze współrzędnych punktu A i B

	y2−y1
a=
	x2−x1

Przez środek przekatnej przechodzi prosta prostopadła na której leży druga przekątna kwadratu

	−1
Jej współczynnik kierunkowy a2=
	a

Umiesz policzyć a i środek ?

Jolanta: Pewnie jesteś zajęta a za chwilę muszę wyjsc

	yc−ya		−1
a=		=....=
	xc−xa		2

Prosta na której leży druga przekątna ma a=2

	xa+xc
y=2x+b należy do niej środek przekatnej xs=		=....1 ys=3
	2

3=2*1+b. b=1 y=2x+1 na tej prostej leży B I D Trzeba obliczyć długość przekątnej − wzór na długość odcinka Połowa to odległość środka od szukanego B I D

Jolanta: |AC|=√(x_c−x₎²+(y_c−y_a)² = ........=√80

1
	√80=√1/4*√'80=√20. Odległość od środka przekatnej(1;3) do wierzchołka (D lub E)
2

√20=√(x_d−x_s,)²+(y_d,−y,_s,)². /² 20=x_d²−2x_d+1+y_d²−6y_d+9 (podstawilam x_s=1 y_s = 3) Prosta ma równanie y=2x+1 podstawiamy za y 20=x²−2x,+1+(2x+1)²−6(2x+1)+9 20=x²−2x+1+4x²+4x+1−12x−6+9 5x²−10x−15=0. /:5 x²−2x−3=0 Δ=16 x₁=−1 x₂=3 y₁=2*(−1)+1=−1 y₂=2*3+1=7 B(−1;−1). D(3;7)

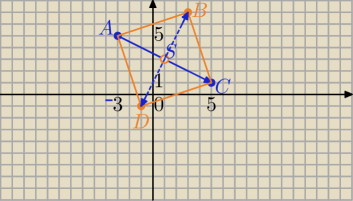
Mila: Przekątne kwadratu są równe i prostopadłe AC^→=[8,−4]

1
	AC→=[4,−2]
2

S=(1,3)− środek AC [4,−2] ⊥[2,4] oraz [4,−2]⊥[−2,−4] S=(1,3)→T_[2,4]= (3,7)=B S=(1,3)→T_[−2,−4]=(−1, −1)=D

Jolanta: Ale rozwiąza ma być bez wektorow

basia: Jolanta dziękuję pięknie. O takie rozwiązanie mi chodziło. JESTEŚ WIELKA

Mila: Przepraszam, oglądam film i niedokładnie czytam treść