omj świruś: https://www.omj.edu.pl/uploads/attachments/2etap19r.pdf w zadaniu nr 4 jak oni wywnioskowali, że skoro pq=bc to nm=1/2 *bc

ABC: odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i jego długość to połowa długości tego boku co z ciebie za bokser jak tego nie wiesz....

świruś: już doszłam do tego przed chwilą dzięki jak zwykle za miłe słowo

ABC:   Amicus Plato sed magis amica veritas

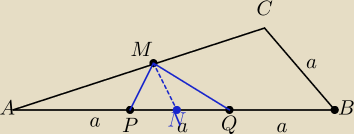
Mila: Dany jest trójkąt ABC, w którym AB =3·BC. Punkty P i Q leżą na boku AB i speł− niają warunek AP = P Q = QB. Punkt M jest środkiem boku AC. Wykaż, że <) P M Q = 90◦. 1) MN||BC⇒

	1		1
N jest środkiem odcinka AB i MN=		|BC|=		a
	2		2

N jest środkiem odcinka |PQ|=a czyli MN jest środkową ΔPQM Jeżeli środkowa trójkąta równa się połowie boku, do którego została poprowadzona, to trójkąt jest prostokątny. |∡PMQ|=90^o

świruś:

chichi: to co napisała @Mila oczywiście jest prawdą, ale wynika to suchy fakt, ktory wynika z równie krótkiego jak ten niebieski zapis uzasadnienia Twoim zadaniem jest napisac to uzasadnienie

świruś: ale że tutaj mam napisać ? czy ogólnie, że trzeba pisać te uzasadnienia

chichi: no skoro nie potrafisz zapisac uzasadnienia tych slow, to nie jest to dla ciebie oczywisty fakt, wiec sama bys z niego w rozwiązaniu nie skorzystala..

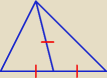
świruś: jak okrąg na tym opiszesz to będzie to kąt oparty na średnicy co tu udowadniać ?

chichi: to jest wlasnie uzasadnienie tego niebieskiego faktu, widze ego powirowało