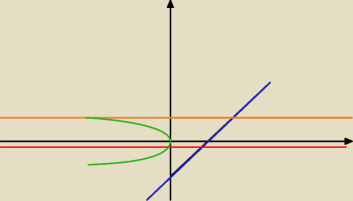
Pole obszaru Koperta: Oblicz pole obszaru ograniczonego krzywymi y²=−x y=x−6 y=−1 y=4 Podzielilem ten obszar na 3 częsci Pierwsza to −16>0 ∫4−√−x dx = 64/3 Druga to trapez a=5=b=10h=5 co się równa 37 i 1/2 I trzecia to ten mały kawałek ograniczany przez −√−x oraz y=−1 I w tym wyszło mi ⁴₃−²ⁱ₃ Całki liczyłem kalkulatorem całek wiec raczej bez błedu rachunkowego Wychodzi mi wynik z liczbą zespoloną i nie wiem czy to dobrze pomoze ktos?

ABC z roboty: nie może w liczbach rzeczywistych wyjść wynik z liczbą zespoloną

Koperta: To w jaki sposób podzielić ten obszar? Bo nie napisalem ale podzieliłem go rysując prostą x=0 i przez to powstały te 3 częsci

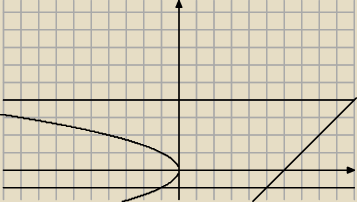
wredulus_pospolitus: dlatego nie używa się kalkulatora jeżeli nie potrafisz samemu policzyć ∫₋₁₆⁰(4 − √−x)dx + ∫₀⁵(4 − (−1))dx + ∫₅⁹( 4−(x−6) )dx − ∫₋₁⁰ (−1 − (−√−x) )dx = = ∫₋₁₆⁰(4 − √−x)dx + ∫₀⁵(4 − (−1))dx + ∫₅⁹( 4−(x−6) )dx + ∫₋₁⁰(1 − √−x )dx = ...... co dalej można byłoby przekształcić tak aby nie mieć √−x zmieniając odpowiednio granice całkowania

kerajs: P=∫₋₁⁴ ((y+6)−(−y²))dy=...