udowodnij
kajtusiek:
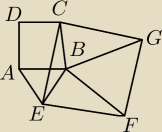
Na zewnątrz kwadratu ABCD, na boku AB, zbudowano trójkąt równoboczny ABE. Następnie utworzono
taki kwadrat CEFG, że punkt B leży wewnątrz niego (może nie widać tego na rysunku tak dobrze
ale bardzo się starałem to narysować ).Udowodnij, że trójkąt BFG jest równoboczny.
10 sty 03:17
chichi:
rysunek:
https://zapodaj.net/plik-zc5uExh1QG
(1) odkładamy ΔCBE na boku EF, u mnie to ΔEHF
(2) ΔHEB − równoramienny z kątem 60
o przy wierzchołku → ΔHEB − równoboczny
(3) stąd ΔBHF równoramienny, pondat |∡BHF| = 150
0 ⇒ |∡HBF| = 15
o = |∡HFB|
(4) no i mamy zatem, że |∡BFG| = 60
o
(5) analogicznie postępując na drugim boku otrzymamy, że |∡BGF| = 60
o
(6) wniosek → ΔBGF − równoboczny □
P.S. (5) można zastąpić przystawaniem ΔBEF do ΔBCG z cechy bkb.

10 sty 04:32
10 sty 23:10
chichi:
o rane boskie... ale przyznaj, że jak na maturę i zadanie na 3 pkt. to dosyć solidne zad

10 sty 23:15
Janek: chichi skad przejscie z (3) do (4) ? z góry zakładasz że przystają EHF i BHF. Wg mnie
niekompletny dowód.
11 sty 15:16
Janek: zmieniam zdanie

11 sty 15:26
Mila:
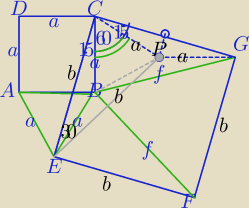
b=f
11 sty 17:19
Mila:
Zadanie z kwadratem ( z kątem 150o) było w Nowej Erze, było na forum wrzucone.
Kto rozwiązał to , mógł sobie szybko poradzić bez trygonometrii.
Sposobem chichi, albo jak pokazałam .
11 sty 18:52
 Na zewnątrz kwadratu ABCD, na boku AB, zbudowano trójkąt równoboczny ABE. Następnie utworzono
taki kwadrat CEFG, że punkt B leży wewnątrz niego (może nie widać tego na rysunku tak dobrze
ale bardzo się starałem to narysować ).Udowodnij, że trójkąt BFG jest równoboczny.
Na zewnątrz kwadratu ABCD, na boku AB, zbudowano trójkąt równoboczny ABE. Następnie utworzono
taki kwadrat CEFG, że punkt B leży wewnątrz niego (może nie widać tego na rysunku tak dobrze
ale bardzo się starałem to narysować ).Udowodnij, że trójkąt BFG jest równoboczny.



 b=f
b=f