dana jsst parabola werdi: Dana jest parabola o równaniu y=x² + 4. Przez punkt P = (0, m) poprowadzono dwie styczne do tej paraboli. Wyznacz wartości parametru m, dla których poprowadzone styczne są prostopadłe. Zapisz obliczenia.

. : No dobrze. Masz jakiś pomysł? Zrobiłaś rysunek?

werdi: rysunek zrobiłem ale nie wiem co mam zrobić dalej

wredulus_pospolitus: zauważ, że punkty styczności oraz punkt P wyznaczają Ci trójkąt prostokątny. Dodatkowo możesz zauważyć, że punkt P leży na symetralnej paraboli. Dodatkowo parabola jest funkcją wypukłą. Związku z tym (nie wiem na jakim jesteś poziomie nauczania i związku z czym jest to zadanie) można mocno ułatwić sobie to zadanie zauważając, że te dwie styczne będą względem siebie symetryczne względem osi OY. Więc punkty styczności będą miały współrzędne (x_o , x_o² + 4) oraz (−x_o, x_o² + 4). Co daje nam długość przeciwprostokątnej tego trójkąta równą 2x_o. Dodatkowo wiemy, że ten trójkąt prostokątny będzie także równoramienny. Związku z tym, będzie on połową kwadratu, więc odległość od punktu P do przeciwprostokątnej (wysokość trójkąta) będzie równa połowie przeciwprostokątnej, czyli równa x_o. Ale także wiemy, że jest to równe: x_o² + 4 − m Związku z tym wiemy, że m = x_o² − x_o + 4. Teraz możemy wyznaczyć współrzędne punktów korzystając ze wzoru na styczną do wykresu, przechodzącą przez tak wyznaczone współrzędne punktu P.

werdi: nie rozumiem ale dzięki

Ala: Mógłby ktoś wytłumaczyć to zadanie bardziej i je dokończyć bo nie rozumiem niestety?

. : Ale którego albo od którego punktu nie rozumiesz / nie rozumiecie? Po pierwsze − porządny rysunek jest do tego potrzebny.

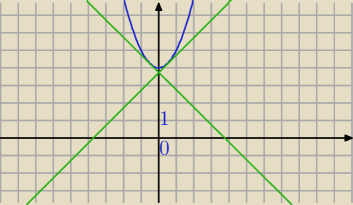
Mila: 1) m<4 A=(x₀,f(x₀) ) lub B=(−x₀, f(−x₀) ) punkty styczności ( OY jest osią symetrii paraboli) f(x)=x²+4 s: y=f'(x₀)*(x−x₀)+f(x₀) f'(x)=2x

	−1
2) Styczne prostopadłe⇔f'(x0)=
	f''(−x0)

	−1
2x0=
	−2x0

4x₀²=1

	1		−1
x0=		lub x0=		=
	2		2

2.1

	1
x0=
	2

	1		17
f(±		)=
	2		4

	1		1		17
s1: y=2*		(x−		)+
	2		2		4

	15
y=x+
	4

=======

	1
x0=(−		)
	2

	1		1		17
s2: y=2*(−		)*(x+		)+
	2		2		4

	15
s2 : y=−x+
	4

===========