dane jest rownanie maks: Dane jest równanie (x + 3)(x²+ m² −2m − 8) = 0 z niewiadomą x i parametrem m ∊ R. Wyznacz wszystkie wartości parametru m, dla których to równanie ma trzy różne rozwiązania rzeczywiste, które tworzą ciąg arytmetyczny.

wredulus_pospolitus: podam taki sposób podejścia do tematu: zapiszmy: W(x) = (x+3)(x² + m² − 2m − 8) więc mamy trzy możliwości (dla r > 0), aby rozwiązania naszego równania tworzyły ciąg arytmetyczny: 1. W(x) = (x+3 − r)(x+3)(x+3 +r) 2. W(x) = (x+3 − 2r)(x+3 − r)(x+3) 3, W(x) = (x+3)(x+3+r)(x+3+2r) weźmy pierwszy przypadek i wymnóżmy dwa nawiasy zawierające 'r': 1. W(x) = (x+3)[ (x+3)² − r²] = (x+3)( x² + 6x + 9−r² ) niemożliwe do spełnienia (bo w wyjściowej postaci wielomianu nie ma w tym nawiasie czynnika z 'x' weźmy drugi przypadek 2. W(x) = (x+3)(x² + 6x − 3rx + 9 −9r + 2r²) teraz widzimy, że musi zajść: 6x − 3rx = 0 −−−> 3r = 6 −−−> r = 2 więc nasz W(x) = (x+3)(x² −1) −−−> więc m² − 2m − 8 = −1 −−> m² − 2m − 7 = 0 Δ ... i wyznaczasz 'm'. weźmy trzeci przypadek 3. W(x) = (x+3)(x² + 6x + 3rx + 9 +9r + 2r²) teraz widzimy, że musi zajść: 6x + 3rx = 0 −−−> 3r = 6 −−−. r = −2 ale przyjęliśmy, że r>0, więc przypadek bez rozwiązania.

maks: czemu przyjęliśmy r>0? co jak nie przyjmiemy

wredulus_pospolitus: jak nie przyjmiemy r>0 to (2) i (3) przypadek oznaczają to samo zauważ, że dla r<0 przypadek (2) reprezentuje dokładnie to samo co dla (r>0) przypadek (3). I na odwrót (oczywiście).

wredulus_pospolitus: więc albo dwa przypadki bez założenia r>0 (tylko r≠0 ). albo 3 przypadki przy założeniu r>0.

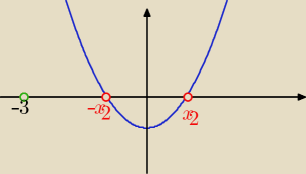
Eta: Można też tak: x₁= −3 równanie x²+m²−2m−8=0 ma dwa rozwiązania różnych znaków gdy m²−2m−8 <0 ⇒m∊(−2,4) i są nimi −x₂ i x₂ (położone symetrycznie względem osi Oy aby wszystkie trzy tworzyły ciąg arytmetyczny to −3,−x₂,x₂ ⇒ x₂=1 i f(−3)≠0 ⇒m≠ 1 ( bo nie mogą być −3,−3,3 zatem −3,−1,1 −− tworzą ciąg arytm r= 2 więc m²−2m−8 = −1 ( bo x²−1=0 ⇒ x=−1 v x= 1 dlaΔm= 32 Odp: m= 1−2√2 v m= 1+2√2 bo ( obydwa m∊(−2,4)\{1} ========================

Eta: i jeszcze 2 przypadek −x₂, −3, x₂ −−− c.arytm daje sprzeczność −6=0

wredulus_pospolitus: @Eta ... w tym rozwiązaniu brakuje mi wyjaśnienia (którego raczej uczeń nie będzie w stanie samemu napisać −−− więc będzie jasne dla nauczyciela, że nie on rozwiązał to zadanie) skąd wiemy, że pozostałe dwa rozwiązania MUSZĄ być symetryczne względem osi OY. A to też jest konieczne, aby w konsekwencji przejść do tego, że pozostałe rozwiązania będą w zbiorze liczb całkowitych (a to także nie jest tak oczywiste dla ucznia)

Eta: Równanie x²+c=0 jest sprzeczne dla c>0 ma dwa rozwiązania x₁= −√c, √c dla c<0 a takiej postaci jest w tym zadaniu równanie x²+m²−2m−8=0 c= m²−2m−8 Nie wiem,co tu nie jest jasne

wredulus_pospolitus: @Etuś ... mam nadzieję, że nie bierzesz tego za czepianie się ... po prostu Ty to wiesz ... ja to wiem ... ale uczeń ... eeeee, niekoniecznie

Jolanta: (x+3=0 x=−3 sprawdzam czy nastepny wyraz ciągu jest mniejszy czy większy od −3 podstawiam −3 (−3)²+m²−2m−8=0 m²−2m+1=0 Δ_m=4−4=0 dla x=−4 (−4)²+m²−2m−8=0 m²−2m+8=0 Δ_m=4−32=−28 Δ_m<0 brak pierwiastków x=−3 jest mniejsze od nastepnego wyrazu r>0 −3, −3+r ,−3+2r wyrazy ciagu arytmetycznego (−3+r)²+m²−2m−8=0 (−3+2r²+m²−2m₈=0

Jolanta: (−3+r)²+m²−2m−8=0 (−3+2r)²+m²−2m−8=0 9−6r+r²+m²−2m−8=0 9−12r+m²−2m−8=0 m²−2m+r²−6r+1=0 \(−1) m²−2m+4r²−12r+1=0 −m²+2m−r²+6r−1=0 m²−2m+4r²−12r+1=0 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 3r²−6r=0 3r(r−2)=0 r≠0 r=2 −3+2=−1 −1+2=1 dla x=−1 i x=1 x²=1 1+m²−2m−8=0 m²−2m−7=0 Δ_m=32

	2−4√2
m1=		=1−2√2
	2

m₂=1+2p{2]