wykaz ze
pola: Wykaż, że dla dowolnych liczb rzeczywistych x i y takich, że x2 + y2 ≤ 1 , prawdziwa jest
nierówność y≤x2+1
8 sty 20:38
chichi:
spałem dziś 2h, więc nie będę wymyślał sprytnie, a zrobimy to łopatologicznie...
dla y < 0 nierówność jest oczywiście spełniona, więc trzeba zbadać co się dzieje dla y ≥ 0,
ponadto wiemy, że y ≤ 1 zatem mamy równoważnie pokazać, że: ∀
x∊R x
2 − y + 1 ≥ 0
Δ = 4(y − 1) ≤ 0 dla 0 ≤ y ≤ 1, co oczywiście kończy dowód

8 sty 21:02
jc:
y2 ≤ 1 − x2 ≤ 1
dlatego y ≤ 1
ale 1 ≤ 1+ x2
a więc y ≤ 1+x2
8 sty 21:02
ABC:
niewprost : przypuśćmy że y>x2+1 , to y>1 , to y2>1 , to x2+y2>1 sprzeczność z założeniem
8 sty 21:04
pola: to jak bo już nie rozumiem
8 sty 21:43
jc: tak, jak pisze ABC jest najprościej
(u mnie, aby nie było luk, też w jednym miejscu należałoby działać nie wprost; gdzie?)
8 sty 22:21
wredulus_pospolitus:
@pola ... piękno matematyki polega na tym, że przeważnie istnieje więcej niż jedna droga 'do
celu'

Masz podane dwa różne sposoby poradzenia sobie z tym problemem.
Przestudiuje oba i wybierz ten który jest dla Ciebie zrozumiały.
8 sty 22:45
Maciess:
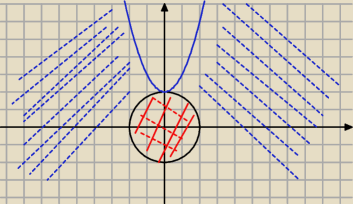
Obrazek niepowiązany

8 sty 22:52

 Masz podane dwa różne sposoby poradzenia sobie z tym problemem.
Przestudiuje oba i wybierz ten który jest dla Ciebie zrozumiały.
Masz podane dwa różne sposoby poradzenia sobie z tym problemem.
Przestudiuje oba i wybierz ten który jest dla Ciebie zrozumiały.
 Obrazek niepowiązany
Obrazek niepowiązany 