Wykaż, że r = r1 + r2 + r3 hlerric: Wewnątrz trójkąta ABC wybrano dowolny punkt M, przez który poprowadzono proste równoległe do jego boków. Proste te podzieliły trójkąt ABC na sześć części, z których trzy są trójkątami. Niech r₁, r₂, r₃ będą promieniami okręgów wpisanych w powstałe trójkąty, a r promieniem okręgu wpisanego w trójkąt ABC. Wykaż, że r = r₁ + r₂ + r₃

hlerric: Wiem, że powstałe trójkąty, są do siebie podobne, i należałoby chyba wykorzystać wzór P = p * r

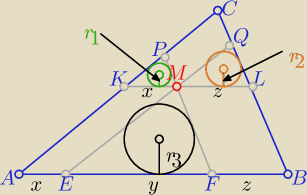
Eta: Z podobieństwa trójkątów z cechy (kkk) ΔKPM ∼ΔABC i ΔQML∼ΔABC i ΔEMF∼ΔABC W skalach

x

r1

z

r2

y

r3

k1=

=

, k2=

=

, k3=

=

x+y+z

r

x+y+z

r

x+y+z

r

	x+y+z		r1		r2		r3
k1+k2+k3=		= 1 to		+		+		=1 /*r
	x+y+z		r		r		r

co daje tezę r₁+r₂+r₃=r ==========

hlerric: @Eta skąd się bierze zapis k₁ + k₂ + k₃ = 1?

Eta:

	x		z		y		x+y+z
k1+k2+k3=		+		+		=		= 1
	x+y+z		x+y+z		x+y+z		x+y+z

jasne?

hlerric: Tak ! Dziękuje